Coupe du Monde 2018: Paul the octopus is back
Enora Belza, Ewen Gallica,b, Romain Gatéa, Vincent Malardéa, Jimmy Merleta, Arthur Charpentiera
aCREM URM CNRS 6211 & Université Rennes 1, bInstitut Louis Bachelier2018-06-23
Résumé
À l’occasion de l’Euro 2008 et de la Coupe du Monde 2010, un poulpe nommé Paul a défrayé la chronique pour ses prévisions exactes des résultats des matchs de l’équipe allemande pour le championnat européen et pour la désignation de l’Espagne comme vainqueur de la compétition mondiale. En utilisant des données sur les résultats de rencontres de Coupe du Monde, compétitions intercontinentales et coupes mondiales, cet article propose de poursuivre le travail de feu Paul le poulpe et de prédire les issues probables des rencontres à venir lors de la Coupe du Monde de football 2018. Huit méthodes d’apprentissage supervisé sont utilisées afin de prédire les résultats des rencontres à venir : les k plus proches voisins, la classification naïve bayésienne, les arbres de classification, les forêts aléatoires, le gradient boosting stochastique, la régression logistique par boosting, les machines à vecteurs de support, les réseaux de neurones artificiels. Les performances relatives de ces méthodes sont présentées, et sont également comparées aux cotes d’un opérateur de paris en ligne. Les résultats sont ensuite utilisés afin de proposer, au moyen de simulations, les trajectoires à venir des équipes nationales au sein de cette compétition.
Mots-clés: Football ; Apprentissage statistique ; Prévisions
1 Introduction
Le football est un sport populaire à travers le monde. On compte, en France, 2,2 millions de licenciés1. Au-delà des aspects ludiques de ce sport, le football occupe une place majeure dans l’industrie du sport et du divertissement. En France, les 43 clubs professionnels ont généré 35000 emplois et plus de 7,5 milliards d’euros de chiffre d’affaires, pour la saison 2015-2016. Ce succès populaire a permis le développement d’une autre activité économique, celle des paris sportifs. Le football représente près de 60% des montants engagés dans l’ensemble des paris sportifs en ligne2.
Histoire des paris sportifs
Bien qu’il soit impossible d’établir l’origine des paris sportifs, les premières preuves remontent à l’Antiquité. Si les paris et jeux d’argent se répandent dans toute l’Europe, la France et l’Angleterre apparaissent comme des terrains particulièrement propices au développement de ces activités. Au 19e siècle, les paris sportifs hippiques remportent un succès considérable. Au 20e siècle, avec l’apparition de la télévision de nouveaux sports commencent à gagner du terrain sur le quasi-monopole du monde hippique. Un nouveau tournant s’est amorcé avec l’apparition d’Internet, début des années 2000. À partir de 2010, les paris en lignes ont été légalement autorisés. Depuis cette période, l’activité est en croissance[^45pctFrancais]. Le chiffre d’affaires total des opérateurs n’a cessé de croître ces dernières années. L’autorité de régulation des jeux en ligne (ARJEL) reporte une augmentation des mises enregistrées au cours du premier trimestre 2018 de 34% relativement au premier trimestre de 20173.
Fonctionnement des paris sportifs
La cote d’un événement sportif est un nombre qui définit à la fois le gain potentiel du parieur et les chances de l’emporter. Il y a donc une relation négative entre la chance de gagner et le gain potentiel, plus il est probable de gagner et plus le gain potentiel est faible. La cote est calculée par l’opérateur de pari en ligne en intégrant les informations disponibles sur un événement sportif. Il est crucial pour un opérateur de pari d’estimer au mieux les probabilités de l’issue d’un événement, afin d’être rentable. Dans le cas du football, la palette des paris sportifs proposés par les opérateurs est large; dans ses formes les plus simples, il s’agit de parier sur l’une des trois issues possibles (victoire, nul, défaite) ou sur le nombre de buts marqués par chaque équipe (le score final). La littérature s’est penchée sur ces deux types de paris, en développant deux approches statistiques distinctes afin de prédire les probabilités associées aux issues possibles, en utilisant les résultats des rencontres précédentes. La première approche consiste à estimer le nombre de buts qui devrait être marqué par chaque équipe, et donc le score final. Cette branche de la littérature se base sur des méthodes de régression. La deuxième approche consiste à estimer directement les probabilités associées à chaque issue possible, ces méthodes sont dites de classification. Récemment, ces dernières ont connu un développement considérable.
Objectif
L’objectif de cet article est d’explorer plusieurs méthodes statistiques afin de prévoir les issues des rencontres sportives, dans le cas de la Coupe du Monde 2018. Nous nous intéressons à la comparaison des performances relatives de ces méthodes, et les combinons pour les confronter aux prévisions des opérateurs de paris en ligne.
Cet exercice permet de faire des prédictions sur l’issue la plus probable, pour chaque rencontre. Au moyen de simulations l’exploitation des résultats permet également de retracer les trajectoires les plus probables, pour chaque équipe nationale en compétition. Les simulations permettent également pour chaque équipe de prédire sa probabilité d’aller en finale et de gagner la Coupe du Monde.
Le reste de cet article est organisé de la façon suivante. La section 2 propose une revue de la littérature relative à la prédiction résultats de matchs. La section 3 décrit les données utilisées par les modèles présentés dans la section 4. La section 5 s’attache à mesurer la qualité prédictive des modèles. Enfin, la section 6 présente les résultats des prévisions.
2 Revue de littérature prédiction et paris sportifs
Historiquement, la littérature relative à la prédiction des résultats de matchs s’est penchée sur la modélisation des scores des rencontres, au moyen de modèles de comptage. Une approche «directe», consistant à modéliser non plus le nombre de buts inscrits lors d’un match par chacune des deux équipes, mais le résultat final de la rencontre (victoire, nul ou défaite) a été adoptée plus récemment par un pan de la littérature. Des modèles statistiques dits «classiques», de type probit ont d’abord été employés à cet effet ; puis, plus récemment, en lien avec la remise au goût du jour et le développement des techniques liées au big data, par des méthodes d’apprentissage statistiques. Que la prédiction porte sur le nombre de buts ou sur l’issue d’un match, elle est à l’origine d’une activité économique importante, celle des paris sportifs.
Cette section donne dans un premier temps un aperçu des techniques de modélisation des scores à l’aide de modèles de comptages, puis des méthodes plus récentes visant à classifier l’issue des rencontres. Une revue de littérature de l’utilisation de ces prévisions sur les marchés de paris sportifs et sur son efficience est ensuite proposée.
2.1 Prédiction des scores - modèles de comptage
Moroney (1956) and Reep, Pollard, & Benjamin (1971) utilisent les distributions Poisson et Binomiale Négtive pour modéliser la distribution du nombre total de buts marqués au cours d’un match. Maher (1982) développe quant à lui un modèle dans lequel les scores des deux équipes suivent des processus de Poisson indépendants. Le modèle intègre des mesures des capacités de défense et d’attaque des deux équipes. Dans un deuxième temps, afin de corriger la tendance à sous-estimer le nombre de buts l’auteur utilise un modèle Poisson bivarié afin de tenir compte de l’interdépendance des scores des deux équipes. La sous-estimation des nombres de buts se retrouve particulièrement dans la littérature lorsqu’il s’agit de matchs nuls. M. J. Dixon & Coles (1997) proposent une méthodologie pour y remédier. Ils modélisent les scores au moyen de lois de Poisson indépendantes, mais, pour les matchs présentant de faibles scores, les auteurs ajustent les probabilités de façon ad hoc de façon à augmenter les probabilités de matchs nuls (0–0 et 1–1). Les auteurs introduisent également une fonction de pondération pour diminuer la contribution des matchs les plus anciens.
Des modèles de Poisson bivariés améliorés peuvent permettre d’augmenter les probabilités d’obtenir des matchs nuls, c’est notamment l’objet des modèles Poisson bivariés «diagonal inflated», utilisés par Karlis & Ntzoufras (2003).
L’aspect temporel est pris en compte par certaines études, soit en s’intéressant à l’évolution des scores dans une même rencontre, soit en se penchant sur la dynamique des scores de rencontres en rencontres. Ainsi, M. Dixon & Robinson (1998) s’intéressent à la dynamique du score au sein d’un match. Le taux de buts marqués change avec le score, le temps qu’il reste à jouer et l’équipe qui mène (si une des deux équipes mène). Koopman & Lit (2015) utilisent un Poisson bivarié dynamique afin de permettre aux coefficients d’évoluer dans le temps. Enfin, Angelini & Angelis (2017b) proposent un modèle Poisson autoregressif afin de prendre en compte les résultats des derniers matchs et améliorer l’estimation.
2.2 Prédiction des résultats
Une branche de la littérature utilise des modèles de choix discrets (probit ordonné) pour modéliser directement les résultats des matchs sans passer par l’estimation des scores. Cette approche a l’avantage de ne pas être impactée par le problème de l’interdépendance des scores.
Goddard & Asimakopoulos (2004) utilisent un modèle probit ordonné. Le résultat du match entre les équipes \(i\) et \(j\) noté \(y_{ij}\) peut prendre trois valeurs: 0 si l’équipe à l’extérieur gagne, \(\frac{1}{2}\) s’il y a match nul, \(1\) si l’équipe à domicile gagne. L’approche a été utilisée dans plusieurs autres études (Kuypers_2000; Audas, Dobson, & Goddard, 2002 ; Forrest & Simmons, 2000 ; Graham & Stott, 2008 ; Koning, 2000).
Récemment, la littérature s’est penchée sur des méthodes d’apprentissage statistique pour prédire les issues des rencontres. Constantinou, Fenton, & Neil (2013) développent un réseau de neurones bayésien (Bayesian Neural Networks) pour prédire les résultats de matchs. Odachowski & Grekow (2013) prédisent les résultats de matchs à partir des évolutions (dans le temps) des cotes. Les auteurs testent un ensemble d’algorithmes de classification (BayesNet, VotedPerception, Ibk, Bagging, Decision Table, LADTree…). Les auteurs font de la classification sur des résultats binaires (victoire de l’équipe à domicile contre nul ou victoire de l’équipe à l’extérieur; victoire équipe à domicile contre victoire équipe à l’extérieur) et obtiennent une qualité de prédiction de 70%. Tax & Joustra (2015) combinent une analyse en composantes principales (ACP) avec des méthodes de classification “Naive Bayes” et “Multilayer Perceptron”. La qualité de prédiction obtenue est de 54,7%.
Godin, Zuallaert, Vandersmissen, De Neve, & Van de Walle (2014) utilisent des posts twitter et les combinent à de l’information statistique pour améliorer les prédictions de leur modèle.
2.3 Efficience des marchés de paris sportifs
Par analogie avec la littérature sur les marchés financiers, la littérature définit une forme faible de l’hypothèse d’efficience des marchés de paris. Si le modèle de prévision produit de l’information sur les probabilités de résultat d’un match qui n’est pas déjà reflétée dans les cotes établies par les bookmakers, alors les cotes échouent à satisfaire le critère standard d’efficience de forme faible: toute l’information historique pertinente pour l’évaluation des probabilités de résultat d’un match devrait être reflétée dans les cotes établies (Goddard & Asimakopoulos, 2004).
Pankoff (1968) est le premier à mettre en place un test d’efficience des marchés de paris. Le test consiste à régresser les résultats des matchs (mesurés par la différence de buts marqués) sur les cotes des bookmakers. Pope & Peel (1989) testent l’hypothèse d’efficience faible des marchés de paris sur le football anglais, en régressant les résultats des matchs sur les probabilités implicites (calculés à partir des cotes définies par les bookmakers). Leurs résultats semblent indiquer que l’hypothèse d’efficience n’est pas toujours vérifiée.
Une autre approche pour tester l’hypothèse d’efficience des marchés consiste à générer des prédictions pour obtenir des probabilités associées à chaque résultat, et identifier les meilleures opportunités de paris (M. J. Dixon & Coles, 1997 ; Goddard & Asimakopoulos, 2004 ; Koopman & Lit, 2015 ; Rue & Salvesen, 2000). Les résultats de ces études suggèrent des formes d’inefficiences faibles.
Spann & Skiera (2009) montrent qu’une qualité de prédiction de 53.98% peut être suffisante pour mettre en place une stratégie de paris profitable. Angelini & Angelis (2017a) étudient l’efficience des marchés sur un ensemble de 11 championnats européens, et trouvent que 4 championnats apparaissent inefficients, suggérant la possibilité de paris rentables.
3 Les données
Pour prévoir les résultats de la Coupe du Monde de Football 2018, il est nécessaire de rassembler des données sur les rencontres footballistiques passées, à la fois sur les rencontres elles-mêmes, mais également sur des caractéristiques propres à chaque équipe. Pour savoir comment s’inscrivent nos prévisions relativement à celles issues des marchés de paris sportifs, il convient également de récupérer des informations au sujet des cotes. Cette section s’attache à présenter succinctement les sources et quelques statistiques descriptives des données utilisées dans cette étude.
3.1 Rencontres internationales
La Fédération Internationale de Football Association (FIFA) communique les résultats, mois par mois, des rencontres passées4. Pour chaque rencontre, les informations suivantes sont disponibles : le lieu, la date, les équipes qui s’affrontent, le type de match (amical, coupes diverses) et le résultat final.
Nous récupérons les données des rencontres masculines allant d’août 1993 à avril 2018, c’est-à-dire juste avant la coupe du Monde 2018 en Russie. Bien que les données des rencontres amicales soient proposées par la FIFA, seules celles de compétitions (phases de qualifications et phases finales) entre les nations composent l’échantillon utilisé dans cette étude. En effet, les enjeux lors des matchs amicaux ne sont pas les mêmes que lors de tournois entre les nations. Les informations des rencontres amicales servent uniquement lors du calcul de la forme d’une équipe (présentée plus loin). L’échantillon concerne 205 équipes et contient 11584 rencontres uniques, dont 6479 provenant de compétitions intercontinentales et 5105 issues des coupes mondiales (Coupes du Monde, Coupes des Confédérations). La Figure 1 montre la répartition du nombre de matchs par année, pour les coupes intercontinentales et pour les coupes mondiales.
Figure 1. Nombre de rencontres par année par type de compétition.
3.2 Caractéristiques des équipes
Chaque observation correspond à une rencontre entre deux équipes. Les informations propres à chacune de ces rencontres concernent les résultats, le classement des équipes ainsi que leur forme.
3.2.1 Classement
Lors d’un match de football, l’issue de la rencontre est fonction de la différence de classement existant entre les deux équipes qui s’affrontent. Une manière de tenir compte de la différence entre les forces des deux équipes est de se fier au Classement mondial de la FIFA, publié depuis août 1993. Ce classement permet de comparer les équipes entre elles, en prenant en compte, entre autres, les résultats passés de chaque équipe ainsi que la valeur des adversaires rencontrés5. La Figure 2 reporte l’historique du classement, par équipes (par défaut, toutes les équipes sont présentes sur l’affichage, il suffit de cliquer dans la barre de recherche pour sélectionner une ou plusieurs équipes à afficher).
Figure 2. Classement FIFA.
3.2.2 Forme
Durant une compétition qui se déroule sur une poignée de semaines, le niveau d’une équipe peut-être altéré en fonction des victoires ou défaites récentes, qui viennent définir la forme d’une équipe. Le classement FIFA, reflétant le niveau relatif de chaque équipe sur les 12 derniers mois, ne peut de facto pas permettre de capter la variabilité de la forme d’une équipe sur une courte période. Il peut alors s’avérer utile d’introduire des mesures de la forme de chaque équipe. Trois indicateurs sont proposés. Un premier inspiré de Goddard & Asimakopoulos (2004), indique simplement l’issue des précédentes rencontres (victoire, nul ou défaite), en retenant uniquement les trois derniers matchs. Les deux indicateurs restants indiquent la forme offensive et la forme défensive de chaque équipe, en calculant la moyenne pondérée du nombre de buts inscrits et concédés, respectivement, lors des trois derniers matchs. La pondération retenue accorde plus d’importance aux matchs les plus récents6. Il faut noter que les calculs effectués pour définir la forme des équipes s’appuient également sur les résultats des rencontres amicales.
Des statistiques descriptives des différences de classement et de forme des équipes s’étant rencontrées sont proposées dans le tableau ci-après.
Tableau 1. Statistiques descriptives sur les classements et formes des équipes.
3.2.3 Autres caractéristiques
Lors de l’estimation, les modèles peuvent s’appuyer sur d’autres caractéristiques propres aux rencontres et aux équipes qui s’affrontent.
Concernant les rencontres en elles-mêmes, quatre prédicteurs sont présents. Le premier indique le type de la rencontre : compétition mondiale ou intercontinentale. Le second mesure la phase de jeu et indique si cette dernière est préliminaire ou non. Les deux autres prédicteurs renseignent l’année du match et le mois. La variable ajoutée pour les mois est introduite pour prendre en compte des effets de saisonnalité éventuels.
Pour les équipes, leur date de fondation est ajoutée, tout comme le continent qu’elles représentent. Enfin, une indicatrice par équipe est créée, pour chacune des 20 premières au dernier classement FIFA. Pour celles classées en deçà de la 20e position, une variable catégorielle supplémentaire est créée pour les désigner.
3.3 Marchés sportifs
La mise en confrontation des estimations réalisées par les différents modèles qui sont présentés dans la section suivante avec celles des sites de paris sportifs est un moyen de repérer les matchs pour lesquels un gain financier est possible. Pour cela, il faut récupérer les cotes des rencontres pour lesquelles l’on désire effectuer des pronostics. À l’aide de techniques de scraping, les cotes pour les rencontres de phases de groupes de la Coupe du Monde 2018 en Russie ont été récupérées pour le site Betclic, le 11 mai 2018.
4 Les modèles
Cette analyse fait face à un problème de classification. Il s’agit, à partir d’observations de rencontres footballistiques passées, de réaliser une segmentation de ces premières. Pour ce faire, chacun des huit modèles envisagés dans cette étude procède globalement de manière identique, en cherchant à trouver les facteurs permettant de segmenter au mieux les rencontres en fonction des trois résultats possibles : victoire de l’équipe 1, match nul, victoire de l’équipe 2. Cette section fournit des intuitions pour l’ensemble des modèles estimés. De plus amples détails sont disponibles dans les références suivantes : Berk (2016), Murphy & Bach (2012) ou encore Charpentier, Flachaire, & Ly (2018).
Il sera fait mention dans les explications qui suivent de classes pour les rencontres. Il faut entendre par là qu’un match peut appartenir à trois classes différentes : victoire de l’équipe 1, match nul, victoire de l’équipe 2.
4.1 Deux modèles simples
Deux premiers modèles de classification sont estimés.
4.1.1 K plus proches voisins
La méthode des K-Nearest Neighbors (ou k plus proches voisins), est une méthode non paramétrique simple pouvant être utilisée à la fois pour des problèmes de régressions ou de classification. L’algorithme des k plus proches voisins s’appuie sur les similarités qui peuvent exister entre les caractéristiques d’observations hors échantillon (des matchs futurs, par exemple), et celles d’obsvervations intraéchantillon (des matchs déjà passés, dont on connaît le les résultats). Ces similarités permettent de définir, pour les observations hors échantillon, quelle classe leur attribuer, en fonction des classes connues des observations avec des caractéristiques proches. En clair, ici, l’issue d’un match futur est prédite en choisissant la classe la plus fréquemment observée parmi les \(k\) matchs aux caractéristiques les plus proches de la rencontre future. Les résultats seront sensibles à la valeur de \(k\) qui sera à déterminer lors de l’estimation, et à la méthode retenue pour mesurer la distance entre les observations (voir section suivante).
4.1.2 Classification naïve bayésienne
La méthode Naive Bayes (ou classification naïve bayésienne) est une méthode de classification basée sur le théorème de Bayes, dans laquelle une hypothèse “naïve” sur l’indépendance entre les caractéristiques (ici, les variables permettant de réaliser une classification de l’issue des rencontres) est faite. Dans le cadre des matchs de football, une victoire de l’équipe 1 peut être fonction de trois caractéristiques (pour simplifier) : de la forme de l’équipe, de son classement, de la différence de classement entre les deux équipes. Ces caractéristiques peuvent être liées dans la réalité, mais il est supposé avec la méthode de classification naïve bayésienne qu’il n’en est rien, que ces trois caractéristiques sont indépendantes. L’intérêt d’une telle hypothèse est de pouvoir simplifier grandement les calculs de la probabilité conditionnelle d’appartenir à une classe pour une rencontre. En effet, cette probabilité conditionnelle peut, sous cette hypothèse, se calculer comme le produit des probabilités de chaque caractéristique (c.-à-d. les probabilités marginales). Pour reprendre l’exemple précédent, la probabilité d’avoir une victoire de l’équipe 1 conditionnellement aux trois caractéristiques précédemment citées, se calcule en multipliant : (\(i\)) la probabilité d’avoir une victoire de l’équipe 1 conditionnellement à la forme de l’équipe, (\(ii\)) la probabilité d’avoir une victoire de l’équipe 1 conditionnellement au classement de l’équipe, et (\(iii\)) la probabilité d’avoir une victoire de l’équipe 1 conditionnellement à la différence de classement entre les deux équipes. Chacune de ces trois probabilités s’obtient facilement, en effectuant des divisions. Par exemple, pour la première, il suffit de compter, pour une forme donnée de l’équipe, le nombre victoires de l’équipe 1, et de diviser ce résultat par le nombre de rencontres disputées pour cette forme donnée. En pratique, plutôt que de considérer une forme donnée, il est plus judicieux de choisir des voisins proches, qui ont une forme similaire. L’estimation des probabilités de chaque caractéristique est alors réalisée par noyau, ce qui nécessite de choisir a priori une distribution pour le noyau et une valeur pour la fenêtre. Cette dernière peut être sélectionnée dans une étape de tuning (voir section suivante).
4.2 Arbres de classification
Les arbres d’analyse et de régression (aussi appelés arbres de décision, dont l’acronyme est CART) sont des régressions dont les prédicteurs sont des variables indicatrices. Les résultats sont présentés sous forme de structures en forme d’arbres. Durant l’estimation, les prédicteurs sont transformés en variables indicatrices puis sont sélectionnés petit à petit. Les variables continues sont transformées en indicatrices. Par exemple, ici, la variable de forme offensive de l’équipe (qui est, rappelons-le, un comptage du nombre moyen de buts inscrits lors des trois dernières rencontres) est transformée en une multitude de variables possibles : 0 but contre 1 ou plus ; 1 but contre 0, 2 ou plus, moins de 2 buts contre plus de 2 buts, etc. Les variables catégorielles sont pour leur part regroupées. Par exemple, pour la variable indiquant le continent de l’équipe, une liste (non exhaustive) de regroupement serait la suivante : Europe contre le reste, Afrique contre le reste, Afrique et Europe contre le reste, etc. Une fois que chaque variable soumise pour l’estimation a été transformée en ces multitudes de regroupements, le problème est double : (\(i\)) choisir, pour chaque variable, quel est le meilleur regroupement à effectuer pour discriminer au mieux les données (au regard d’un critère particulier), et (\(ii\)) choisir, parmi les variables disponibles, celles qui discrimine le mieux les données. Une fois la variable et son découpage sélectionnés, il résulte deux sous parties dans les données, deux branches, donnant lieu à deux noeuds. Dans chacune de ces branches, une nouvelle étape de sélection de variables munie de son découpage/regroupement est effectuée de manière séparée, pour découper à nouveau en deux les sous-échantillons. Cette étape itérative se poursuit pour chaque branche, tant qu’un nouveau découpage est jugé pertinent au regard du critère. Chaque noeud terminal indique les proportions d’observations (c.-à-d. de matchs) appartenant à chacune des classes (c.-à-d. les issues de rencontres). L’assignation d’une classe à match ayant les caractéristiques conduisant à l’appartenance à un noeud spécifique est alors déterminée en fonction des fréquences de classes observées dans ce noeud : si une majorité de matchs nuls est observée dans le noeud, alors il sera prédit un match nul pour la rencontre appartenant à ce noeud.
4.2.1 Bagging et arbres de classification
Dans le but d’augmenter les performances d’estimation des arbres de décisions, il est possible de s’appuyer sur un ensemble de résultats et de les agréger pour produire un résultat final. Cette technique, qui n’est pas restreinte aux arbres de décisions, s’appelle le bagging (ou l’ensachage). Le bagging (contraction de “Bootstrap Aggregation”) fonctionne de la manière suivante. ll s’agit de tirer un échantillon aléatoire avec remplacement dans les données à disposition (un “échantillon bootstrap”). Ensuite, un modèle CART est estimé. Une classe est attribuée à chaque noeud terminal, comme expliqué précédemment, et la classe affectée à chaque cas ainsi que les valeurs des prédicteurs dans le voisinage sont stockées. Ensuite, un nouvel échantillon est tiré et l’on recommence cette procédure. On réitère de nombreuses fois. Puis, une fois ces itérations réalisées, pour chaque observation du jeu de données initial, il suffit de compter le nombre d’arbres désignant cette observation dans chacune des classes. La classe finale d’une observation est alors désignée en fonction de la fréquence de classe désignée la plus haute. Comme la valeur des prédicteurs associée à chaque noeud est également stockée, il est possible d’effectuer des prédictions à partir de données hors de l’échantillon, en leur associant dans un premier temps le noeud final de chaque arbre, puis en assignant une classe finale en s’appuyant à nouveau sur les fréquences de classes désignées.
4.2.2 Forêts aléatoires
Les Random Forest (ou forêts aléatoires) s’appuient sur les techniques de bagging précédemment évoquées. L’algorithme de cette méthode d’apprentissage fonctionne de la manière suivante. Dans un premier temps, un échantillon boostrap est tiré du jeu de données. Dans un second temps, un échantillon aléatoire sans remplacement des prédicteurs est tiré. Puis, une première partition des données en deux sous-échantillons est effectuée, comme expliquée précédemment. Les partitions suivantes sont réalisées en tirant à nouveau des prédicteurs sans remplacement, jusqu’à obtenir un arbre d’une taille désirée. Les proportions des noeuds finaux sont ensuite calculées. La classification, à l’aide de l’arbre ainsi obtenu est effectuée pour les données du jeu n’étant pas dans l’échantillon tiré (on appelle ces données “out of bag”), et est réservée en même temps que les valeurs des prédicteurs associées aux noeuds. Toutes ces étapes sont ensuite réalisées de nombreuses fois pour obtenir un ensemble de résultats. En utilisant les fréquences d’appartenance à une classe pour chaque observation, il est alors possible de décider la classe prédite.
4.3 Boosting
Le boosting est une technique fondée sur l’agrégation d’un ensemble de modèles estimés de manière itérative, apprenant des erreurs commises à chaque itération. Il s’agit d’accorder des poids plus importants aux observations ayant été mal prédites par le modèle lors de l’itération précédente pour construire la nouvelle estimation. Contrairement au bagging, les prévisions ne sont pas faites de manière indépendante, mais séquentielles.
4.3.1 Gradient Boosting stochastique
Le Gradient Boosting (GBM) est un algorithme de boosting qui s’appuie sur l’optimisation du gradient associé à une fonction de perte (par exemple, la fonction de perte quadratique). À chaque itération de l’algorithme, un arbre de régression est estimé pour estimer le gradient de la fonction de perte, afin de fournir une direction pour la descente effectuée, visant à faire décroître la fonction de perte (on parle de descente de gradient). La longueur de la descente peut être déterminée en faisant appel à la méthode du point de col (ou steepest descent), afin de réduire au maximum la fonction de perte. Une contrainte est toutefois appliquée pour la longueur de la descente, de manière à avoir un apprentissage lent.
Les étapes du stochastic gradient boosting sont les suivantes. Dans un premier temps, à partir de l’échantillon d’apprentissage, il s’agit d’estimer un premier modèle pour prédire la classe des rencontres de cet échantillon. La suite consiste à estimer de manière itérative des modèles en prenant compte des erreurs commises lors des estimations précédentes. Plus précisément, pour une itération donnée, il s’agit de calculer dans un premier temps, pour chacune des observations de l’échantillon, le gradient associé à la perte quadratique. Puis, un sous-échantillon sans remplacement dans les données est tiré. À partir des valeurs négatives de gradient associées aux données contenues dans ce sous-échantillon, un arbre de régression est estimé, pour un nombre de noeuds prédéterminé. La prévision dans chacun des noeuds terminaux (les stumps) de cet arbre est ensuite calculée, de manière à minimiser les erreurs. Les résultats de ce nouvel arbre peuvent alors être ajoutés aux résultats issus de l’itération précédente, pour venir mettre à jour le modèle. Les itérations prennent fin soit à l’issue d’un nombre prédéterminé de tours, soit à l’aide d’une mesure (comme l’erreur quadratique moyenne) permettant d’éviter les effets de surapprentissage.
4.3.2 Régression logistique par boosting
La régression logistique par boosting est une technique de boosting dans laquelle la fonction de coût utilisée est une fonction logit. Les arbres de régression estimés à chaque itération ne contiennent qu’un seul noeud.
4.4 Support Vector Machine
Les Support Vector Machines (SVM) (ou Machines à vecteurs de support) sont des modèles d’apprentissage supervisés utilisés pour effectuer des régressions ou des classifications. L’idée des SVM est de trouver un hyperplan optimal permettant de catégoriser les observations (en dimension deux, il s’agit de trouver une droite séparant le plan en deux). Deux cas sont distingués : celui dans lequel il est possible d’effectuer une séparation linéaire, et celui dans lequel il est nécessaire d’avoir recours au préalable à une transformation des données dans un nouvel espace, à l’aide d’une fonction noyau. En règle général, il existe plusieurs hyperplans pouvant séparer les données. L’algorithme se charge de trouver une solution optimale, qui maximise la marge ; la marge étant la distance séparant les points proches de la zone de décision de cette dernière (l’hypersurface permettant de séparer l’espace vectoriel en deux).
4.5 Réseaux de neurones
Les Artifical Neural Networks (ou réseaux de neurones artificiels) sont inspirés de la manière dont l’information est transmise dans le système nerveux en neurosciences. Le principe est de combiner de manière non linéaire des entrées pour obtenir des sorties. L’objet de l’estimation porte sur l’apprentissage de la fonction permettant de combiner les entrées pour obtenir les bonnes sorties. Les réseaux de neurones contiennent une succession de couches que l’on peut décomposer en trois parties : (\(i\)) une couche d’entrée, (\(ii\)) des couches intermédiaires cachées, et (\(iii)\) une couche de sortie. Les sorties d’une couche sont utilisées dans la suivante comme entrée, après avoir été combinées (des poids sont attribués à chaque valeur et un biais est ajouté) puis soumises à une fonction d’activation. Cette fonction d’activation, qui tente de mimer le fonctionnement du cerveau (le neurone doit-il être activé ou non ?) peut prendre différentes formes. Par exemple, il peut s’agir d’une fonction seuil. Dans ce cas, si la valeur après obtenue après combinaison est en dessous d’un seuil, la sortie est nulle (le neurone n’est pas activé) ; sinon, elle vaut 1 (le neurone est activé). Il existe d’autres fonctions d’activations, qui ne retournent pas des valeurs binaires, mais des sorties comprises entre 0 et 1, comme la fonction sigmoïde par exemple.
5 Les estimations : fait-on mieux qu’un poulpe ?
À l’occasion de l’Euro 2008 et de la Coupe du Monde 2010, un animal a défrayé la chronique pour ses prévisions exactes des résultats des matchs de l’équipe allemande pour le championnat européen et pour la désignation de l’Espagne comme vainqueur de la compétition mondiale. Cet animal, un poulpe nommé Paul, a donné lieu à de nombreuses tentatives par la suite de faire prédire le score des rencontres de tournois à des animaux. Talents divinatoires, ou pure coïncidence ? Notre but n’est pas de trancher sur cette question. En revanche, il est intéressant de mesurer la qualité prédictive des modèles qui ont été estimés à l’aide des données historiques, en la comparant avec ce que pourrait donner un animal effectuant un choix purement aléatoire. Pour ce faire, cette section propose une description de la méthodologie employée pour réaliser l’estimation des modèles présentés dans la section précédente, puis s’attache à présenter les résultats des estimations en mettant l’accent sur la qualité des prédictions.
5.1 Création d’échantillons
Pour éviter des effets de surapprentissage, c’est-à-dire d’avoir des modèles surajustés, qui correspondent trop aux données ayant servi à l’estimation, mais donnant de piètres performances avec de nouvelles données, une approche par validation croisée a été adoptée.
Dans une première étape, nous divisons l’échantillon en deux parties ; l’une contient 80% des données, l’autre, appelé «échantillon de validation», les 20% restants.
5.2 Estimations sur l’échantillon de test
La première partie va servir à estimer les modèles et à choisir les variables et paramètres permettant d’obtenir les meilleures prévisions au sein de cet échantillon comprenant les 80% d’observations. Cette étape de tuning (ou d’ajustement des paramètres) est réalisée de la manière suivante. Pour des valeurs données de paramètres, un modèle est estimé par validation croisée de type k-fold. Plus précisément, sur l’échantillon contenant 80% des observations, un découpage en \(k=10\) sous-échantillons de taille à peu près identiques est réalisé. Un premier sous-échantillon est mis de côté (l’échantillon de test) tandis que les 9 restants (échantillons d’apprentissage) servent à estimer le modèle avec les paramètres choisis. Une fois l’estimation achevée, le modèle est utilisé pour prévoir les valeurs à partir des informations contenues dans le 10e sous-échantillon placé de côté. Des mesures de qualité de la prévision sont alors calculées, puis stockées (pour choisir les meilleures valeurs de paramètres à utiliser, nous utilisons la mesure Log-Loss, basée sur l’entropie, permettant d’évaluer le taux de dissimilarité entre les vraies issues de la rencontre et celles prédites). Un second des 10 sous-échantillons est mis de côté et l’estimation du modèle est de nouveau réalisée à partir des 9 sous-échantillons restants, les prévisions sont comparées avec les valeurs de ce second échantillon et les mesures d’erreur sont à nouveau stockées. Puis le troisième sous-échantillon devient la référence permettant de tester l’estimation, et ainsi de suite jusqu’à ce que chacun des 10 sous-échantillons ait servi de test. À ce moment, pour réduire les erreurs de mesures, un nouveau découpage en 10 sous-échantillons de tailles à peu près identiques est effectué, en tirant aléatoirement les observations figurant dans chaque sous-échantillon, et les estimations successives sont refaites. Au total, 10 opérations de création de 10 échantillons sont envisagées, ce qui permet de calculer 100 mesures d’erreur/précision pour des paramètres du modèle donnés.
Les paramètres aboutissant au “meilleur modèle” au regard du critère utilisé (ici, Log-Loss) seront retenus. À titre de comparaison, et pour fournir un meilleur aperçu de la qualité d’estimation, d’autres critères sont également calculés. Pour chacun des meilleurs modèles, les 100 valeurs de mesures d’erreur/précision calculées peuvent être représentées graphiquement pour comparer les modèles. C’est ce que propose la Figure 3. Les mesures affichées par des boîtes à moustaches sont les suivantes :
Accuracy: mesure le pourcentage de bonnes classifications (bonnes issues de rencontres). Elle se calcule en comptant le nombre de bonnes classifications sur le nombre total de prévisions. Lorsqu’elle vaut 1, le modèle a bien prédit l’ensemble des classes ; lorsqu’elle vaut 0, le modèle s’est trompé sur toutes les issues des rencontres.Kappa de Cohen: compare la prévision à une prévision aléatoire. Cette mesure s’obtient comme suit : \(\kappa = \frac{\text{Acc} - \text{Acc}_{\text{Exp}}}{1 - \text{Acc}_{\text{Exp}}}\), où \(\text{Acc}_{\text{Exp}}\) est la précision aléatoire prévue. Cette dernière est calculée en faisant la somme des produits des distributions de chaque classe réelles et des distributions prédites ; autrement dit effectuant le calcul suivant : \(\sum_j p_j \times q_j\), avec \(p_j\) la proportion de rencontres de classe \(j\) et \(q_j\) la proportion de rencontres prédites de classe \(j\) (\(j = \{\text{Equipe 1}, \text{Nul}, \text{Equipe 2}\}\)). Plus la valeur de Kappa est élevée, meilleure la classification est, relativement à une classification aléatoire.
La valeur de la fonction Log-Loss précédemment mentionnée est également reportée sur la Figure 3. Comme le montre cette dernière, la précision des modèles est plutôt moyenne et oscille entre 52% de bonnes prévisions pour le modèle k-Nearest Neighbors à 67% pour le modèle Boosted Logistic Regression. Les valeurs du Kappa de Cohen, bien que conservant la même hiérarchie dans le classement des modèles, sont bien inférieures. Ces valeurs faibles s’expliquent par une performance particulièrement mauvaise sur les matchs nuls.
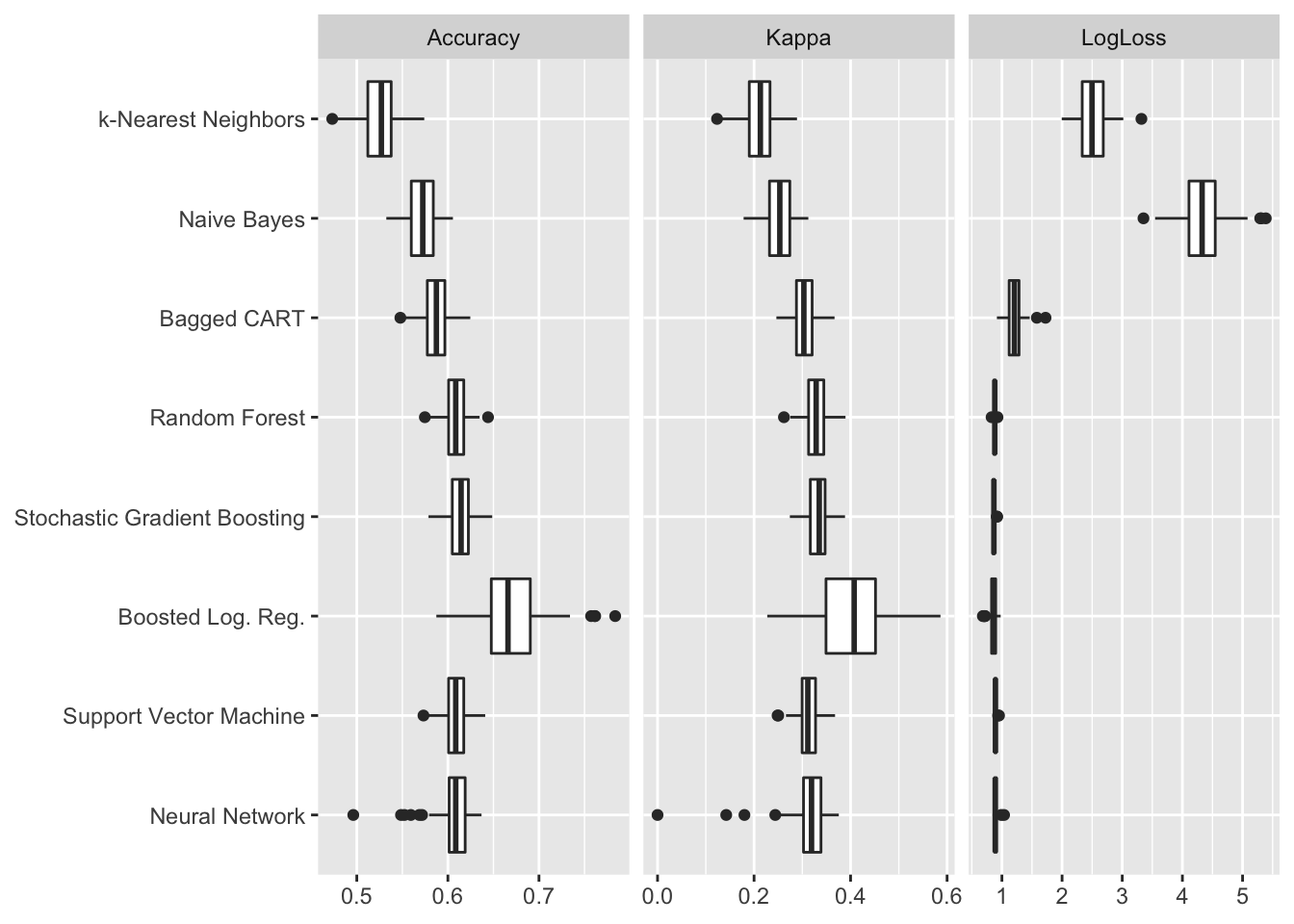
Figure 3. Comparaison des résultats des modèles.
5.3 Estimations sur l’échantillon de validation
L’échantillon de validation, contenant les 20% d’observations n’ayant pas été utilisées jusqu’alors, permet aussi de comparer le comportement des modèles entre eux, en observant cette fois leurs performances respectives pour prédire plus ou moins bien l’issue des rencontres pour des matchs n’ayant pas servi à choisir les paramètres optimaux des modèles respectifs. Nous obtenons des précisions dans les classifications allant de 51.5% à 60.8% en fonction des modèles.
Le Tableau 2 indique, pour chaque modèle, les taux de bonnes prévisions pour chacune des trois classes. On y lit que les bonnes prévisions portent davantage sur les victoires de l’équipe 1 (par exemple, lorsque le vrai résultat est une victoire de l’équipe 1, le modèle Support Vector Machine l’indique dans 87% des cas). Les matchs nuls, qui représentent 21% des rencontres (à la fois dans l’échantillon de validation et dans l’échantillon utilisé pour le paramétrage des modèles) sont très mal prédits : au mieux, lorsqu’il y a effectivement match nul, le modèle k-Nearest Neighbors l’avait prédit dans 17% des cas. Ces mauvaises performances sur les matchs nuls sont courantes dans la littérature (Goddard & Asimakopoulos, 2004).
Tableau 2. Comparaison des taux de bonnes détections.
5.4 Combinaison de modèles : stacking
Une manière souvent utilisée pour améliorer la classification est de procéder à du stacking. Cela consiste à estimer un nouveau modèle, en s’appuyant sur les vraies classes de l’échantillon de test contenant les 80% d’observations et en les estimant par les prévisions obtenues par les modèles estimés précédemment. Ici, nous avons fait appel à une estimation par Gradient Boosting. Une fois ce nouveau modèle estimé, il est possible de comparer les prévisions qu’il effectue sur l’échantillon de validation, et de comparer ses performances avec les modèles précédemment estimés. Les résultats obtenus indiquent une précision dans la classification de l’issue des rencontres de 60.95%, soit légèrement plus que précédemment.
Pour ce qui est du pourcentage de bonnes prévisions pour chaque issue, la combinaison de modèles permet de prédire, lorsque c’est effectivement le cas :
- 85.8% des victoires de l’équipe 1 ;
- seulement 0.6% des matchs nuls ;
- 62.3% des victoires de l’équipe 2.
Le stacking permet donc d’améliorer les prévisions du modèle ici. Par la suite, nous emploierons le terme “combinaison” pour nous référer à ce modèle.
6 Prévision des résultats de la Coupe du Monde 2018
L’intérêt d’avoir entraîné différents modèles pour prévoir l’issue de rencontres footballistiques lors des compétitions est de pouvoir proposer des prévisions pour des matchs qui ne se sont pas encore déroulés. Il faut toutefois garder à l’esprit les erreurs de prévisions mentionnées dans la section précédente. Bien heureux celui qui pourrait prévoir sans se tromper le résultat d’un match.
Avant de proposer les résultats des prévisions, il convient de décrire brièvement la méthode retenue pour les avancer. Les modèles estimés précédemment permettent, lorsqu’on leur fournit de nouvelles données (toutes celles ayant été utilisées pour l’estimation, à l’exception de l’issue de la rencontre, que l’on souhaite prévoir) d’estimer une probabilité de victoire pour chaque équipe ou de match nul. Ces estimations permettent alors de décider de l’issue du match.
Comme les rencontres de la Coupe du Monde ont lieu les unes après les autres et que les modèles se nourrissent des issues des rencontres précédentes, il faut procéder étape par étape. Dans un premier temps, des prévisions pour les premiers matchs de la phase de groupes sont effectuées. Les prévisions pour les matchs suivants sont réalisées après avoir pris note des résultats. De manière synthétique, l’opération suit les étapes suivantes :
- prévisions pour les rencontres au temps \(t\) ;
- mise à jour de la base de données pour prendre en compte les issues des précédents matchs que l’on vient d’estimer ;
- Incrément du temps : \(t\) devient \(t+1\).
Il s’agit de répéter ces trois opérations jusqu’à l’issue de la compétition. Pour l’heure, nos modèles ne prévoient pas le nombre de buts inscrits ou encaissés par les différentes équipes. Aussi, dans les prévisions effectuées, les variables de forme offensive et de forme défensive ne sont pas mises à jour en fonction des résultats des rencontres précédentes durant la simulation de l’avancée du tournoi.
Cette section s’attache à montrer les résultats prévus par les différents modèles, pour les matchs de groupes dans un premier temps, puis pour la totalité de la compétition dans un second temps.
6.1 Prévisions des issues des rencontres de groupes
Le premier décembre 2017, le tirage au sort des huit groupes de la phase de groupes de la Coupe du Monde 2018 a été effectué à Moscou. Chaque groupe est composé de 4 équipes, donnant de facto lieu à 6 rencontres par groupes. Dans un premier temps, les prévisions des deux premiers matchs de chaque groupe sont effectuées. Les résultats prévus sont répercutés dans les données, puis les prévisions sur les deux matchs suivants sont réalisées, et enfin celles sur les deux derniers.
Comme indiqué précédemment, les modèles fournissent une probabilité pour chaque issue possible pour les rencontres (victoire équipe 1, nul, victoire équipe 2). La Figure 3 présente ces probabilités pour chaque rencontre de la phase de groupes. Le menu déroulant en haut à gauche permet de sélectionner la rencontre à afficher (l’utilisation de l’ascenseur à droite de ce menu déroulant est à préférer à la molette d’une souris). Par défaut, les probabilités affichées sont celles issues de la combinaison des prévisions de l’ensemble des modèles (la section précédente ayant montré qu’une combinaison linéaire des prédictions réalisées par l’ensemble des modèles estimés fournit un gain dans le pourcentage de bonnes prédictions) ; le menu déroulant en haut à droite de la figure permet d’afficher les résultats pour chacun des modèles.
Figure 4. Résultats de chaque rencontre de groupe, pour chaque modèle.
6.2 Prévisions des probabilités de gagner la Coupe du Monde 2018
Pour avoir une idée de la probabilité qu’une équipe donnée remporte le titre de champion du monde de football, des simulations de la compétition ont été réalisées. Les résultats de chaque rencontre sont pris en compte avant de simuler les suivantes.
Il convient de préciser comment les issues de chaque rencontre sont déterminées. Pour un match donné, le modèle fournit des probabilités de victoire ou de nul. Une manière de faire serait de retenir l’issue (victoire équipe 1, nul, victoire équipe 2) ayant la probabilité la plus élevée. Cela dit, il peut être intéressant de regarder ce qu’il se passe dans des cas moins probables. Prenons un exemple pour éclaircir ce point. La quatrième rencontre de la Coupe du Monde 2018 opposera le Portugal à l’Espagne. Notre modèle favori donne le Portugal gagnant à 37.17%, l’Espagne à 35.39% et le nul à 27.44%. Dans ce cas précis, il est particulièrement intéressant de considérer ce qu’il peut se passer pour la suite de la compétition en fonction de ces trois issues. Aussi, pour prendre en compte ces éventualités, de nombreuses simulations de la compétition sont effectuées. Dans chaque simulation, pour chaque rencontre, l’issue du match est tirée de manière aléatoire, en attribuant des probabilités d’apparition de la victoire de l’équipe 1, celle de l’équipe 2 ou du nul égales à celles prévues par le modèle. Dans le cas du match Portugal - Espagne, 37.17% des simulations effectuées donneront le Portugal vainqueur, 35.39% l’Espagne et 27.44% indiqueront que le match s’est soldé par un nul.
La manière de déterminer l’issue d’une rencontre ayant été expliquée, il reste à fournir des précisions sur la procédure adoptée pour simuler la chronologie de la compétition. Dans un premier temps, les simulations sont effectuées pour les matchs de la phase de groupes, en suivant la méthode indiquée précédemment. Il est nécessaire de désigner qui, dans chaque groupe se hisse à la première ou à la seconde place au classement ; ces positions étant importantes pour la suite de la compétition. Pour effectuer ce classement, des points sont attribués à chaque équipe à l’issue de chaque rencontre : 3 points en cas de victoire, 1 pour un nul, 0 pour une défaite. À l’issue des prévisions pour l’ensemble des matchs de groupes, le classement dans chaque groupe est effectué, en comptant le nombre de points obtenus sur les trois rencontres que chaque équipe a disputées. En cas d’égalité, le règlement de la FIFA indique que la différence de buts après tous les matchs de groupes fait foi. En cas de nouvelle égalité, le plus grand nombre de buts marqués sert alors à discriminer. S’il persiste encore une égalité, d’autres critères s’appuyant sur les nombres de buts sont utilisés. En dernier ressort, la FIFA prévoir un tirage au sort. Comme les modèles de cette étude ne prévoient pas le nombre de buts, il est impossible d’utiliser les critères normalement applicables, à l’exception du tirage au sort. Aussi, en cas d’égalité au classement pour chaque groupe, un tirage au sort est effectué pour départager les équipes.
Pour les phases suivantes de la compétition, il suffit de suivre le calendrier d’avancement proposé pour la FIFA en se faisant rencontrer en huitièmes de finale les premiers de poules à des seconds : le premier du groupe A contre le second du B, le premier du C contre le second du D, etc. Les vainqueurs poursuivent en quart de finale, puis en demi-finale et enfin en finale.
Le Tableau 3 reporte les résultats des 50 000 simulations ayant été réalisées, en indiquant le pourcentage de tirages (que l’on nomme, par raccourci “Probabilité de Victoire”) dans lesquels chaque équipe est sortie vainqueur de la compétition.
Tableau 3. Estimation de la probabilité de remporter la Coupe du Monde 2018.
6.3 Parcours les plus probables
Grâce aux simulations, il est également possible de se pencher, pour chaque équipe, sur les chances d’être éliminé à chaque phase de la compétition. Il suffit pour cela, pour chaque équipe, de compter le nombre de simulations dans lesquelles elle se fait éliminer dans la phase de groupe, celles dans lesquelles elle sort de la compétition en huitièmes de finale, en quart, en demie ou bien remporte le tournoi. Reste alors à calculer la proportion que chacun de ces événements représente pour chaque équipe. La Figure 5 reporte ces proportions. Le choix de l’équipe s’effectue à l’aide du menu déroulant en haut à gauche de la Figure. On y lit par exemple que dans 20% de nos échantillons, l’Argentine se fait éliminer dès la phase de groupe. Dans 3,65% des cas, elle accède à la Finale et s’incline face à son opposant, tandis que dans 2,25% des simulations elle remporte la coupe.
Il peut également être intéressant de regarder comment évoluent ces chances, conditionnellement à une phase de la compétition déjà effectuée. Quelles sont les chances de l’Argentine de remporter la Coupe du Monde 2018 si elle accède aux quarts de finale ? En sélectionnant la valeur “Huitièmes de Finale” du menu de droite de la Figure 5, le diagramme nous indique la répartition de chaque issue possible, conditionnellement au fait d’avoir réussi à passer les huitièmes de finale. Si l’Argentine a réussi à passer les huitièmes de finale, nos simulations donnent la donnent vainqueur du tournoi dans 12% des cas.
Figure 5. Pourcentage de simulations dans lesquelles l’équipe choisie termine la compétition dans la phase indiquée en abscisse, conditionnellement à la phase de la compétition déjà atteinte (début du tournoi par défaut).
Si les figures précédentes permettent de savoir quelles sont les chances d’une équipe de terminer la compétition dans une phase donnée, elles ne disent en revanche rien sur les adversaires potentiels auxquels elles font face. Pour avoir cette information, il est possible de s’appuyer sur les simulations effectuées pour suivre des parcours possibles pour chaque équipe. La Figure 6 montre, sous la forme d’un arbre (réalisé à l’aide du package collapsibleTree (Khan, 2017)), l’ensemble des parcours ayant été obtenus lors des 50 000 simulations pour chacune des 5 équipes arrivées en tête. L’arbre d’une équipe est composé d’une racine (le nom de l’équipe), de feuilles (les phases de jeu et les adversaires potentiels) liées entre elles par des branches. La taille d’une feuille est proportionnelle au nombre de simulations dans lesquelles l’événement décrit par la feuille a été observé. Ce nombre est indiqué sur la seconde ligne de l’étiquette apparaissant au survol d’une feuille. Ainsi, pour l’arbre de la France (affiché par défaut, utiliser le menu au-dessus du graphique pour afficher l’arbre d’un autre pays) la racine indique que l’arbre fait référence à 50 000 simulations. Les feuilles suivantes indiquent le classement obtenu dans les simulations à l’issue de la phase de groupes : 27 526 cas dans lesquels la France a terminé première de son groupe, 12 755 dans lesquels elle s’est hissée à la seconde place, et 9 735 cas dans lesquels elle n’a pas passé les phases de groupe (7109 troisième et 2626 dernière). En cliquant sur une feuille dont la légende indique le classement à l’issue des matchs de groupe (First, Second, Third ou Fourth), la suite de la compétition s’affiche. Par exemple, en cliquant sur la feuille First pour la France, quatre adversaires potentiels apparaissent pour le huitième de finale : Argentine, Croatie, Islande et Nigeria. La taille de la feuille de la Croatie étant la plus grande, cela traduit le fait que si la France se qualifie pour les huitièmes de finale, son adversaire le plus probable serait la Croatie. En cliquant de feuille en feuille, les différentes possibilités de parcours de la France se révèlent (il est possible d’utiliser le zoom avec la molette de la souris ou du pavé tactile).
Figure 6. Arbres de rencontres simulés pour chacune des 5 premières équipes.
Une autre manière de représenter les différentes possibilités est proposée (cette fois-ci pour chacune des équipes qualifiées à la Coupe du Monde 2018), à l’aide d’un graphique “Rayons de soleil” (ou sunburst, réalisé grâce au package D3partitionR (Guillot et al., 2017)), sur la Figure 7. Après avoir sélectionné une équipe (par défaut, la France est affichée), les différentes phases de la compétition pour cette première sont affichées, sous la forme d’anneaux. Chaque anneau est fractionné proportionnellement au nombre de simulations dans lesquelles l’issue correspondante (qui s’affiche au survol de la souris) s’observe. Lorsque l’on clique sur une portion d’anneau, les portions restantes sont alors masquées pour faciliter la vue et la navigation. Pour afficher à nouveau les anneaux masqués précédemment, il suffit de cliquer sur le cercle central du graphique. À tout instant, il est possible de savoir le chemin parcouru pour aboutir à l’affichage proposé, en suivant les flèches situées en haut du graphique.
Figure 7. Séquences de rencontres simulées par équipe.
Enfin, il est possible de suivre le chemin de chaque équipe, en choisissant l’alternative suivante la plus fréquemment observée dans les simulations. Les résultats sont consignés dans le Tableau 4. On peut y lire que le Brésil gagnerait la coupe. Dans un premier temps, il se hisserait à la première position de son groupe. Puis, il affronterait le Mexique en huitième de finale, remporterait la rencontre et se retrouverait opposé à la Belgique en quart de finale. Après les avoir battus, il disputerait la demi-finale contre la France. Il remporterait ensuite la coupe du monde en vainquant la Suisse.
Tableau 4. Parcours d’équipes durant la compétition.
Il faut noter que ce raisonnement ne traduit pas nécessairement l’issue la plus probable : le parcours s’effectue petit à petit, et de nombreuses issues possibles ne sont donc pas prises en compte une fois qu’un choix a été réalisé. Prenons un exemple pour éclaircir ce point. Considérons une compétition en trois étapes : des matchs de groupe, une demi-finale et une finale. Considérons pour simplifier davantage que 100 simulations ont été effectuées et que les résultats obtenus sont tel qu’indiqué sur la Figure 8. Si l’on suit le raisonnement adopté précédemment pour décrire le chemin d’une équipe au cours de la compétition, il faudra procéder comme suit : l’équipe termine première de son groupe et accède donc à la demi-finale. Sachant cela, elle remportera son match dans 20 simulations et s’inclinera dans 15. On considèrera alors qu’elle accède à la finale, et qu’elle gagnera dans 15 simulations. Aussi, ce parcours le plus probable annoncera cette équipe comme vainqueur du tournoi. Toutefois, il ne s’agit pas de l’issue la plus probable. En effet, si on regarde bien l’arbre, cette équipe perd la compétition dans 83 cas sur 100. Sa probabilité de perdre est bien plus élevée que sa probabilité de gagner. En résumé, le chemin le plus probable n’égale pas nécessairement l’issue de la compétition la plus probable.
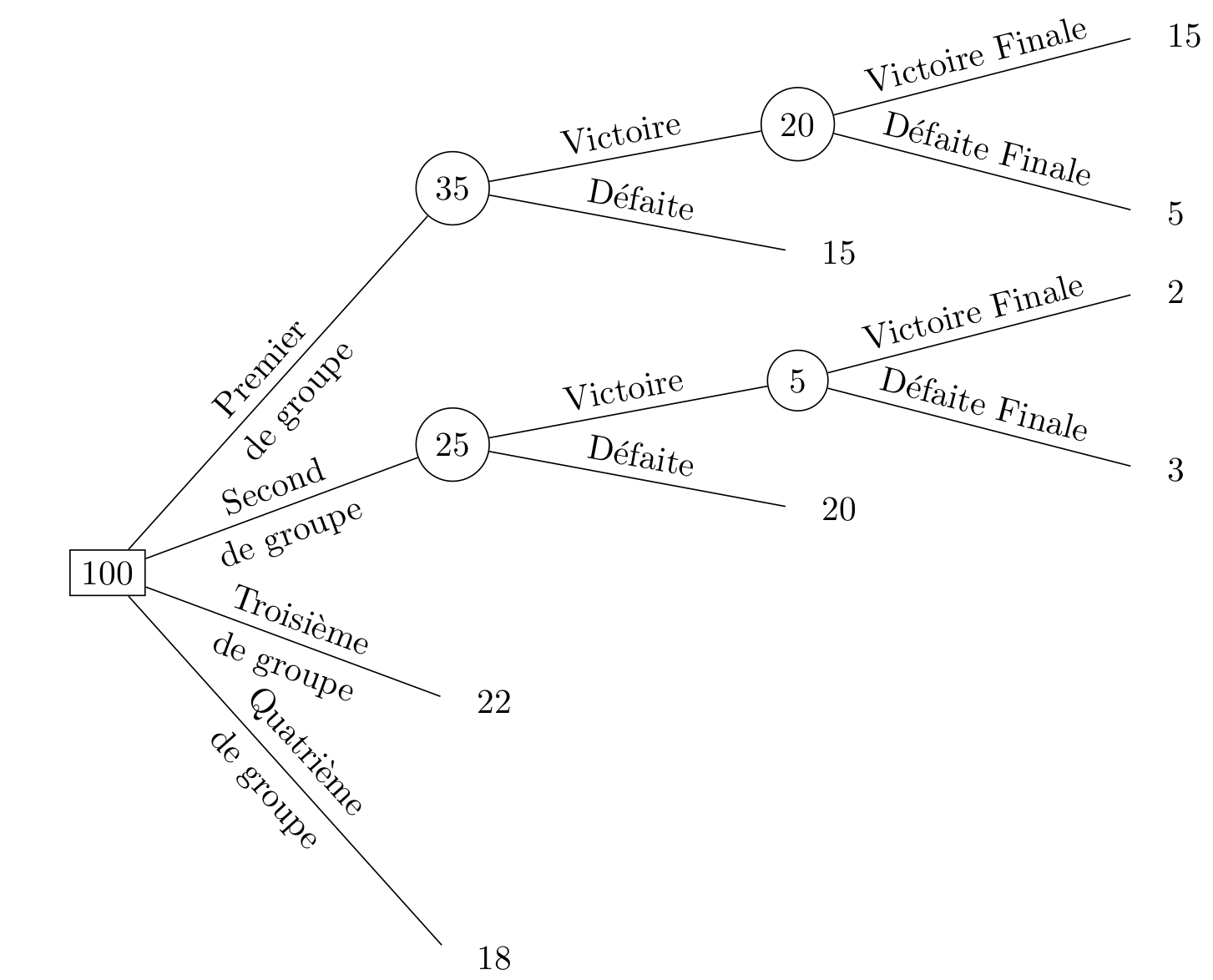
Figure 8. Exemple fictif d’une compétition en trois phases.
6.4 Comparaison avec les prévisions des sites de paris en ligne
La prévision du résultat des rencontres de football à l’issue de 90 minutes de jeu donne lieu à une activité économique importante sur le secteur des paris sportifs. Il semble pertinent de comparer les prévisions établies par nos modèles avec celles que l’on peut observer sur le marché. Pour réaliser un tel exercice, les cotes proposées aux internautes sur le site de paris sportifs Betclic ont été récupérées, comme indiqué dans la section 3.3. Rappelons que pour les paris sportifs, la cote d’un événement exprime l’inverse de la probabilité qu’il se réalise. Autrement dit, si un événement a une probabilité \(p\) d’apparaître, sa cote \(c\) vaut \(c = \frac{1}{p}\). On peut donc retrouver la probabilité associée à la cote d’un événement. Il ne faut toutefois pas négliger un détail important : les sites de paris en ligne conservent une part des sommes misées par les joueurs. La part restante, appelée le taux de retour aux joueurs (TRJ) est redistribuée aux joueurs réalisant des gains. Cette somme, en France, ne doit pas dépasser en moyenne les 85% (pour éviter les adictions au jeu). Aussi, pour chaque cote, si l’on désire avoir une idée de la probabilité estimée, il faut multiplier l’inverse de la cote par le TRJ. Dans notre cas, il y a trois issues : (\(i\)) la victoire de l’équipe 1, avec une probabilité associée \(p_{\text{eq1}}\) et une cote \(c_{\text{eq1}}\) ; (\(ii\)) un match nul, avec une probabilité associée \(p_{\text{nul}}\) et une cote \(c_{\text{nul}}\) ; et enfin (\(iii\)) une victoire de l’équipe 2, avec une probabilité associée \(p_{\text{eq2}}\) et une cote \(c_{\text{eq2}}\). Les cotes sont données, il est nécessaire de déduire le TRJ. Il s’obtient en effectuant le calcul suivant : \[\text{TRJ} = \frac{1}{\frac{1}{c_{\text{eq1}}} + \frac{1}{c_{\text{nul}}} + \frac{1}{c_{\text{eq2}}}}.\] Reste alors à multiplier l’inverse de la cote par ce TRJ pour obtenir la probabilité associée. Par exemple, pour la probabilité associée au match nul : \(p_{\text{nul}} = \frac{1}{c_{\text{nul}}} \times \text{TRJ}\).
Les probabilités associées à chaque issue possible pour chaque match des rencontres de groupes de la coupe du monde sont ainsi calculées. La Figure 9 propose de comparer nos estimations à celles de Betclic, pour chacun des neuf modèles (les huit modèles originaux et la combinaison de ces derniers). Les modèles sont représentés en colonne, les issues des rencontres en ligne. Sur chaque graphique, la bissectrice est tracée. Lorsqu’un point se trouve au-dessus de cette bissectrice, l’estimation que nous avons réalisée est supérieure à celles de Betclic. En revanche, quand un point se situe en dessous de cette bissectrice, notre estimation est inférieure à celle de Betclic.
Dans l’ensemble, notre modèle favori (la combinaison des huit autres) propose des estimations remarquablement proches de celles de Betclic. Les probabilités de victoires pour l’équipe 1 sont très légèrement surestimées relativement à celles de Betclic et les probabilités de victoires pour l’équipe 2 sont très légèrement sous-estimées. Les estimations des matchs nuls sont toutefois nettement sous-estimées dans notre modèle favori, relativement à celles du site de paris sportifs. Les modèles Gradient Boosting et Bagged CART sont en moyenne proches des estimations de Betclic. En revanche, le modèle Naive Bayes propose des estimations assez éloignées de celles du site de paris sportifs. En effet, les estimations de ce modèle sont tranchées : les probabilités associées à chaque issue sont soit proches de 0, soit de 1 et peu d’intermédiaires sont donnés. Aussi, la différence est visible avec les autres modèles et avec les probabilités de Betclic, qui sont davantage réparties entre 0 et 1.
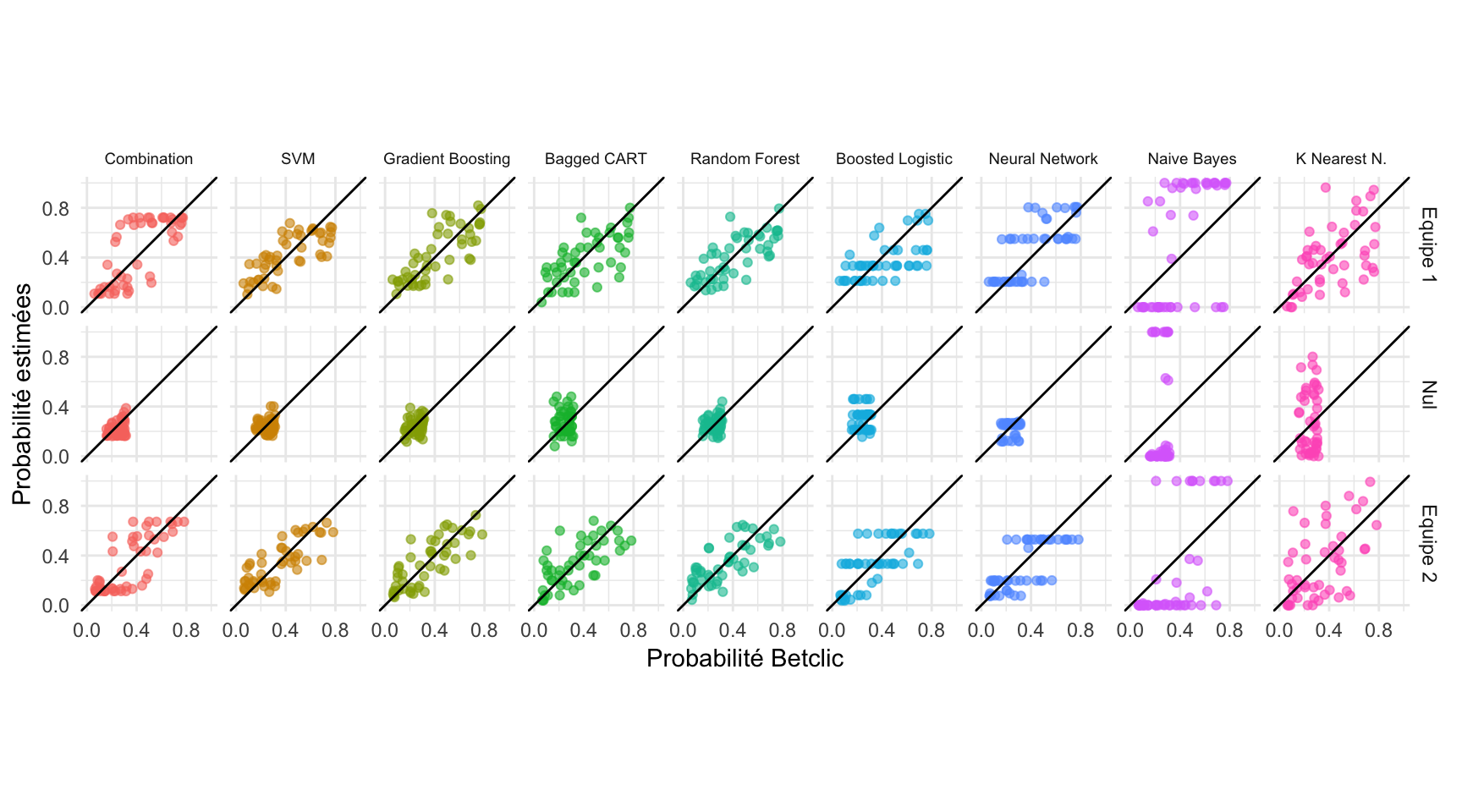
Figure 9. Prévisions des modèles en fonction des prévisions de Betclic.
7 Effet des compositions initiales de groupes sur la probabilité de remporter le tournoi
Le tirage initial déterminant la composition des 8 groupes ainsi que la position de chacune des quatre équipes à l’intérieur de ces groupes a une influence sur l’ensemble la compétition. En effet, ce tirage détermine non seulement les premières rencontres de poules, mais conditionne également les rencontres suivantes. Certaines règles sont imposées par la FIFA lors du tirage au sort pour éviter que les meilleures équipes - au regard du classement FIFA de l’année précédente - se rencontrent avant les quarts de finale. Les règles imposées évitent également que des équipes du même continent se rencontrent en phase de groupes (pas plus d’une équipe de la même confédération dans le même groupe, à l’exception des équipes en provenant de l’UEFA qui peuvent être au maximum 2).
Deux questions se posent alors. Premièrement, en respectant les règles établies par la FIFA, comment un tirage donné favorise-t-il une équipe ou au contraire pénalise une autre ? Deuxièmement, comment les règles appliquées lors du tirage au sort influencent-elles la réussite ou l’échec d’une équipe ?
Pour répondre à ces deux questions, nous proposons d’effectuer de nouvelles simulations. Dans une première série de simulations, 5000 tirages aléatoires respectant les règles de la FIFA sont effectués pour constituer les 8 groupes. Dans une seconde série de simulations, 5 000 autres tirages aléatoires sont effectués, cette fois en n’imposant aucune règle. Une fois les groupes établis, la compétition est simulée 10 000 fois de la même manière que celle présentée dans la section précédente. À l’issue des 10 000 simulation pour un tirage de groupes donné, les probabilités de victoire de chaque équipe sont calculées. La Figure 10 résume ces étapes, pour une équipe.
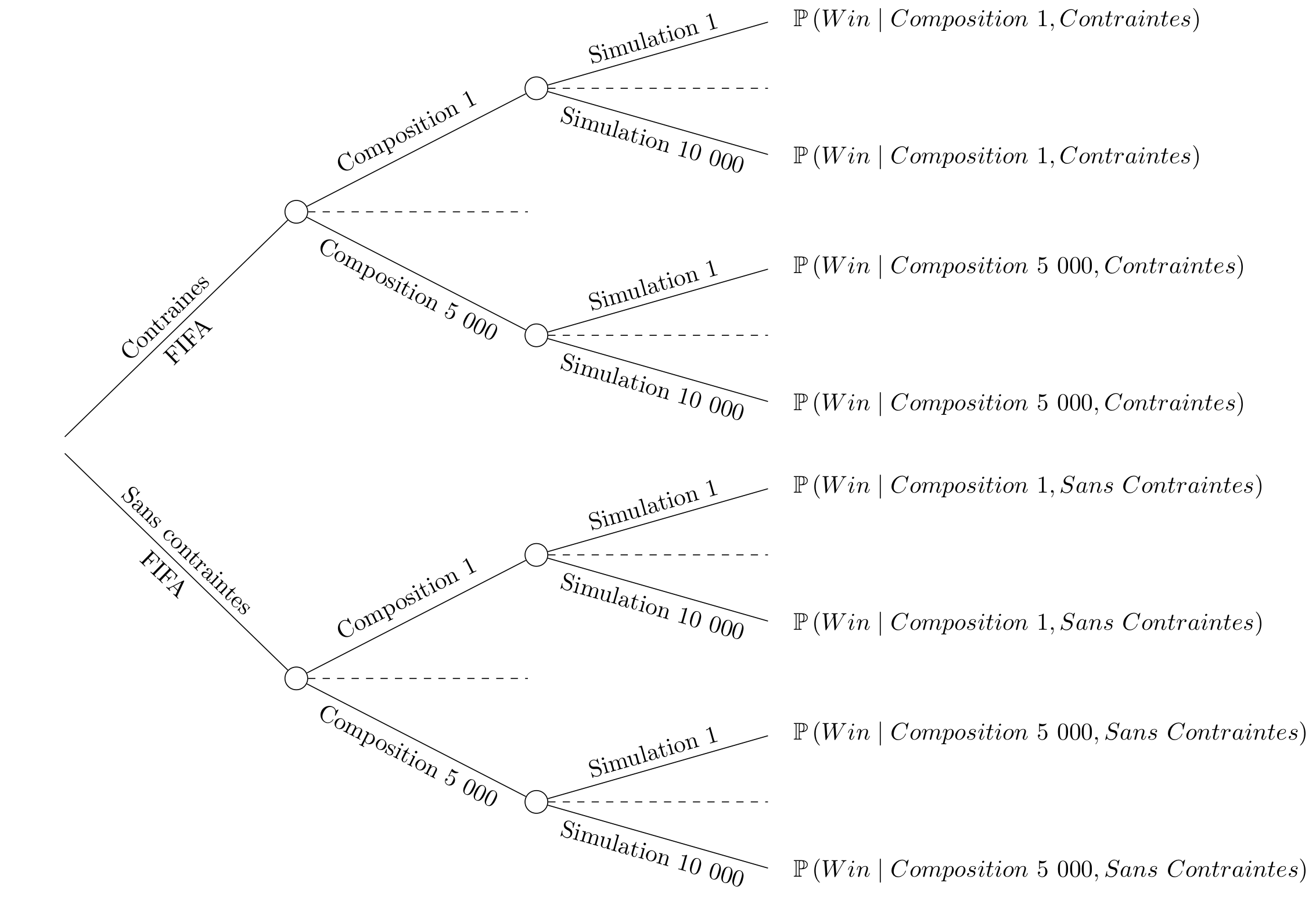
Figure 10. Procédure de simulations.
Une fois que ces simulations sont réalisées, deux tirages sont obtenus comprenant chacun, pour chaque équipe, 5 000 estimations de la probabilités de gagner la compétition conditionnellement à la composition initiale des groupes ; le premier tirage respectant les règles imposées par la FIFA, le second sans contraintes. Ces tirages, aux valeurs contenues entre 0 et 1, peuvent être vus comme des réalisations d’une loi Beta dont les paramètres peuvent être estimés par maximum de vraisemblance. Ainsi, pour chaque équipe et chaque manière de tirer au sort les compositions de groupes, il est possible de comparer la probabilité de gagner de l’équipe sous les conditions réelles de composition des groupes avec la distribution des probabilités de gagner le tournoi conditionnellement à la composition initiale des groupes. Cette comparaison permet de déterminer si une équipe a été avantagée ou au contraire pénalisée par le tirage observé de composition des groupes. La Figure 11 reporte pour chacune des 32 équipes les estimations de densité de la probabilité de remporter la victoire conditionnellement à la composition initiale des groupes, en respectant les règles établies par la FIFA (noir) et en s’en affranchissant (rouge) [pas encore fait]. La probabilité d’observer une probabilité de gagner au moins aussi grande que celle estimée sous les conditions de composition réelle des 8 groupes de la première phase de jeu est indiquée sur chaque graphique. Lorsque cette première est supérieure à 0.5, l’équipe a été désavantagée le vendredi 1er décembre 2017 par le tirage au sort de la composition des groupes. C’est le cas, par exemple, de la plupart des petites équipes.
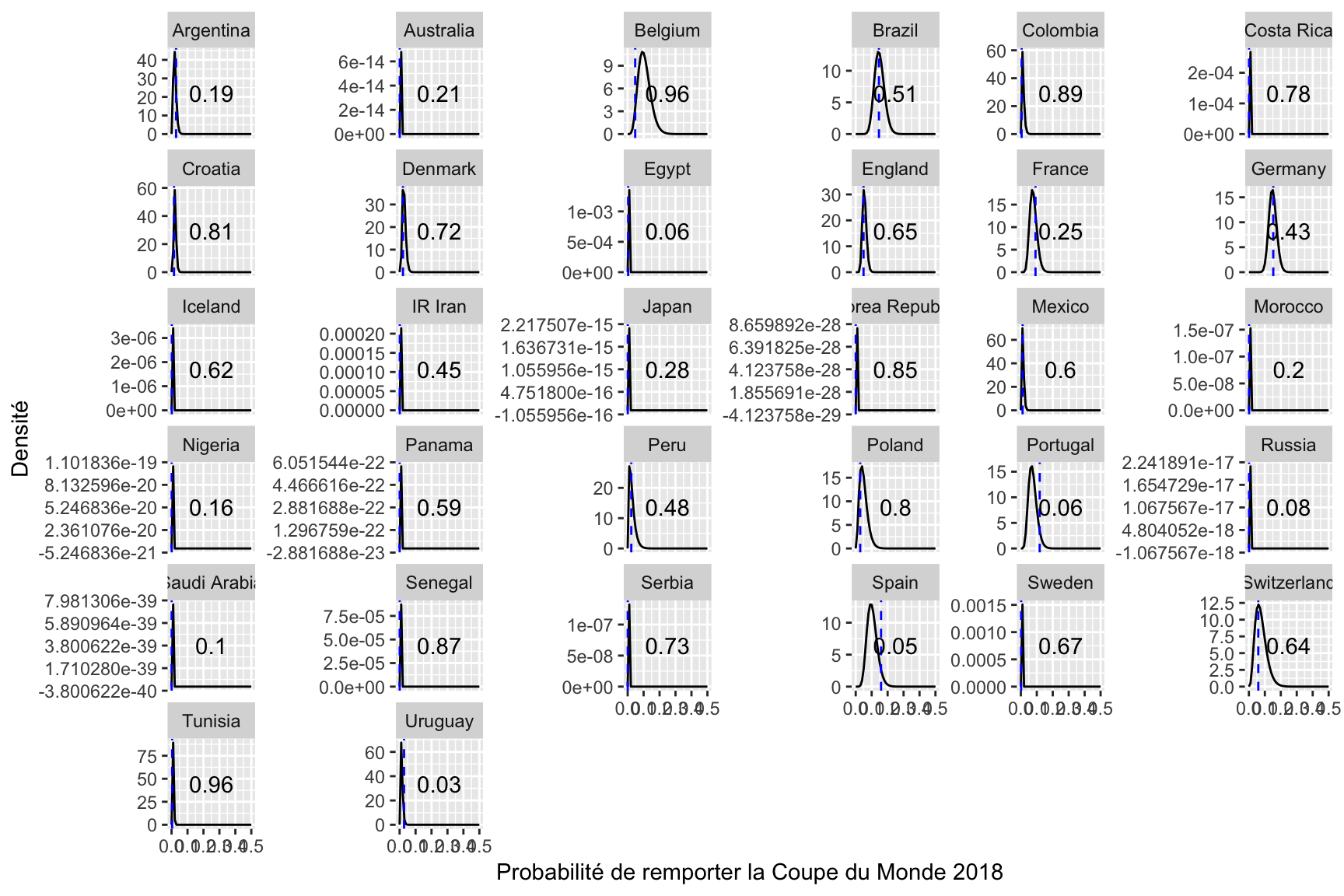
Figure 11. Distribution des probabilités de gagner le tournoi conditionnellement à la composition initiale des groupes
Bibliographie
Angelini, G., & Angelis, L. D. (2017a). Efficiency of Online Football Betting Markets. SSRN Electronic Journal. https://doi.org/10.2139/ssrn.3070329
Angelini, G., & Angelis, L. D. (2017b). PARX model for football match predictions. Journal of Forecasting, 36(7), 795‑807. https://doi.org/10.1002/for.2471
Audas, R., Dobson, S., & Goddard, J. (2002). The impact of managerial change on team performance in professional sports. Journal of Economics and Business, 54(6), 633‑650. https://doi.org/10.1016/s0148-6195(02)00120-0
Berk, R. A. (2016). Statistical Learning from a Regression Perspective. (S.l.) : Springer International Publishing. https://doi.org/10.1007/978-3-319-44048-4
Charpentier, A., Flachaire, E., & Ly, A. (2018, mars). Économétrie & Machine Learning. Manuscrit soumis pour publication. Repéré à https://hal.archives-ouvertes.fr/hal-01568851
Constantinou, A. C., Fenton, N. E., & Neil, M. (2013). Profiting from an inefficient association football gambling market: Prediction, risk and uncertainty using Bayesian networks. Knowledge-Based Systems, 50, 60‑86. https://doi.org/10.1016/j.knosys.2013.05.008
Dixon, M. J., & Coles, S. G. (1997). Modelling Association Football Scores and Inefficiencies in the Football Betting Market. Journal of the Royal Statistical Society: Series C (Applied Statistics), 46(2), 265‑280. https://doi.org/10.1111/1467-9876.00065
Dixon, M., & Robinson, M. (1998). A birth process model for association football matches. Journal of the Royal Statistical Society: Series D (The Statistician), 47(3), 523‑538. https://doi.org/10.1111/1467-9884.00152
Forrest, D., & Simmons, R. (2000). Forecasting sport: the behaviour and performance of football tipsters. International Journal of Forecasting, 16(3), 317‑331. https://doi.org/10.1016/s0169-2070(00)00050-9
Goddard, J., & Asimakopoulos, I. (2004). Forecasting football results and the efficiency of fixed-odds betting. Journal of Forecasting, 23(1), 51‑66. https://doi.org/10.1002/for.877
Godin, F., Zuallaert, J., Vandersmissen, B., De Neve, W., & Van de Walle, R. (2014). Beating the bookmakers: leveraging statistics and Twitter microposts for predicting soccer results. Dans KDD Workshop on Large-Scale Sports Analytics.
Graham, I., & Stott, H. (2008). Predicting bookmaker odds and efficiency for UK football. Applied Economics, 40(1), 99‑109. https://doi.org/10.1080/00036840701728799
Guillot, A., Bostock, M., Lu, S., Rodden, K., Bremer, N., & Spot, H. (2017). D3partitionR: Interactive Charts of Nested and Hierarchical Data with ’D3.js’. (R package version 0.5.0). Repéré à https://CRAN.R-project.org/package=D3partitionR
Karlis, D., & Ntzoufras, I. (2003). Analysis of sports data by using bivariate Poisson models. Journal of the Royal Statistical Society: Series D (The Statistician), 52(3), 381‑393. https://doi.org/10.1111/1467-9884.00366
Khan, A. (2017). collapsibleTree: Interactive Collapsible Tree Diagrams using ’D3.js’. Manuscrit soumis pour publication. Repéré à https://CRAN.R-project.org/package=collapsibleTree
Koning, R. H. (2000). Balance in Competition in Dutch Soccer. Journal of the Royal Statistical Society: Series D (The Statistician), 49(3), 419‑431. https://doi.org/10.1111/1467-9884.00244
Koopman, S. J., & Lit, R. (2015). A dynamic bivariate Poisson model for analysing and forecasting match results in the English Premier League. Journal of the Royal Statistical Society: Series A (Statistics in Society), 178(1), 167‑186.
Maher, M. J. (1982). Modelling association football scores. Statistica Neerlandica, 36(3), 109‑118. https://doi.org/10.1111/j.1467-9574.1982.tb00782.x
Moroney, M. (1956). Facts from Figures, 472 pp. Penguin, Harmondsworth, Middlesex.
Murphy, K., & Bach, F. (2012). Machine Learning: A Probabilistic Perspective. (S.l.) : MIT Press. Repéré à https://books.google.fr/books?id=NZP6AQAAQBAJ
Odachowski, K., & Grekow, J. (2013). Using Bookmaker Odds to Predict the Final Result of Football Matches. Dans Lecture Notes in Computer Science (pp. 196‑205). (S.l.) : Springer Berlin Heidelberg. https://doi.org/10.1007/978-3-642-37343-5_20
Pankoff, L. D. (1968). Market Efficiency and Football Betting. The Journal of Business, 41(2), 203. https://doi.org/10.1086/295077
Pope, P. F., & Peel, D. A. (1989). Information, Prices and Efficiency in a Fixed-Odds Betting Market. Economica, 56(223), 323. https://doi.org/10.2307/2554281
Reep, C., Pollard, R., & Benjamin, B. (1971). Skill and Chance in Ball Games. Journal of the Royal Statistical Society. Series A (General), 134(4), 623. https://doi.org/10.2307/2343657
Rue, H., & Salvesen, O. (2000). Prediction and Retrospective Analysis of Soccer Matches in a League. Journal of the Royal Statistical Society: Series D (The Statistician), 49(3), 399‑418. https://doi.org/10.1111/1467-9884.00243
Spann, M., & Skiera, B. (2009). Sports forecasting: a comparison of the forecast accuracy of prediction markets, betting odds and tipsters. Journal of Forecasting, 28(1), 55‑72. https://doi.org/10.1002/for.1091
Tax, N., & Joustra, Y. (2015). Predicting the Dutch football competition using public data: A machine learning approach. Transactions on Knowledge and Data Engineering, 10(10), 1‑13.
http://www.ey.com/Publication/vwLUAssets/ey-barometre-2017-des-impacts-economiques-et-sociaux-du-football-professionnel/$File/ey-barometre-2017-des-impacts-economiques-et-sociaux-du-football-professionnel.PDF.↩
http://www.fifa.com/live-scores/international-tournaments/fixtures-results/index.html.↩
La pondération est la suivante : 1/2 pour le dernier match, 1/3 pour l’avant-dernier et 1/6 pour l’antépénultième.↩