From Uncertainty to Precision: Enhancing Binary Classifier Performance through Calibration

Séminaire STATQAM – Université du Québec à Montréal

Agathe Fernandes Machado

Université du Québec à Montréal

Arthur Charpentier

Université du Québec à Montréal

Emmanuel Flachaire

Aix-Marseille School of Economics, Aix-Marseille Univ.

🗣️ Ewen Gallic

Aix-Marseille School of Economics, Aix-Marseille Univ.

François Hu

Université de Montréal

1 Introduction

\[ \definecolor{wongBlack}{RGB}{0,0,0} \definecolor{wongGold}{RGB}{230, 159, 0} \definecolor{wongLightBlue}{RGB}{86, 180, 233} \definecolor{wongGreen}{RGB}{0, 158, 115} \definecolor{wongYellow}{RGB}{240, 228, 66} \definecolor{wongBlue}{RGB}{0, 114, 178} \definecolor{wongOrange}{RGB}{213, 94, 0} \definecolor{wongPurple}{RGB}{204, 121, 167} \]

\[\DeclareMathOperator{\g}{g}\]

\[\DeclareMathOperator*{\argmin}{arg\,min}\]

Classification and Confidence

Table 1: Male/Female Classification, using picpurify with images from Hill and White (2020).

female (0.984)	female (0.983)	female (0.982)	female (0.960)
male (0.016)	male (0.017)	male (0.018)	male (0.040)

female (0.009)	female (0.013)	female (0.014)	female (0.015)
male (0.991)	male (0.987)	male (0.986)	male (0.985)

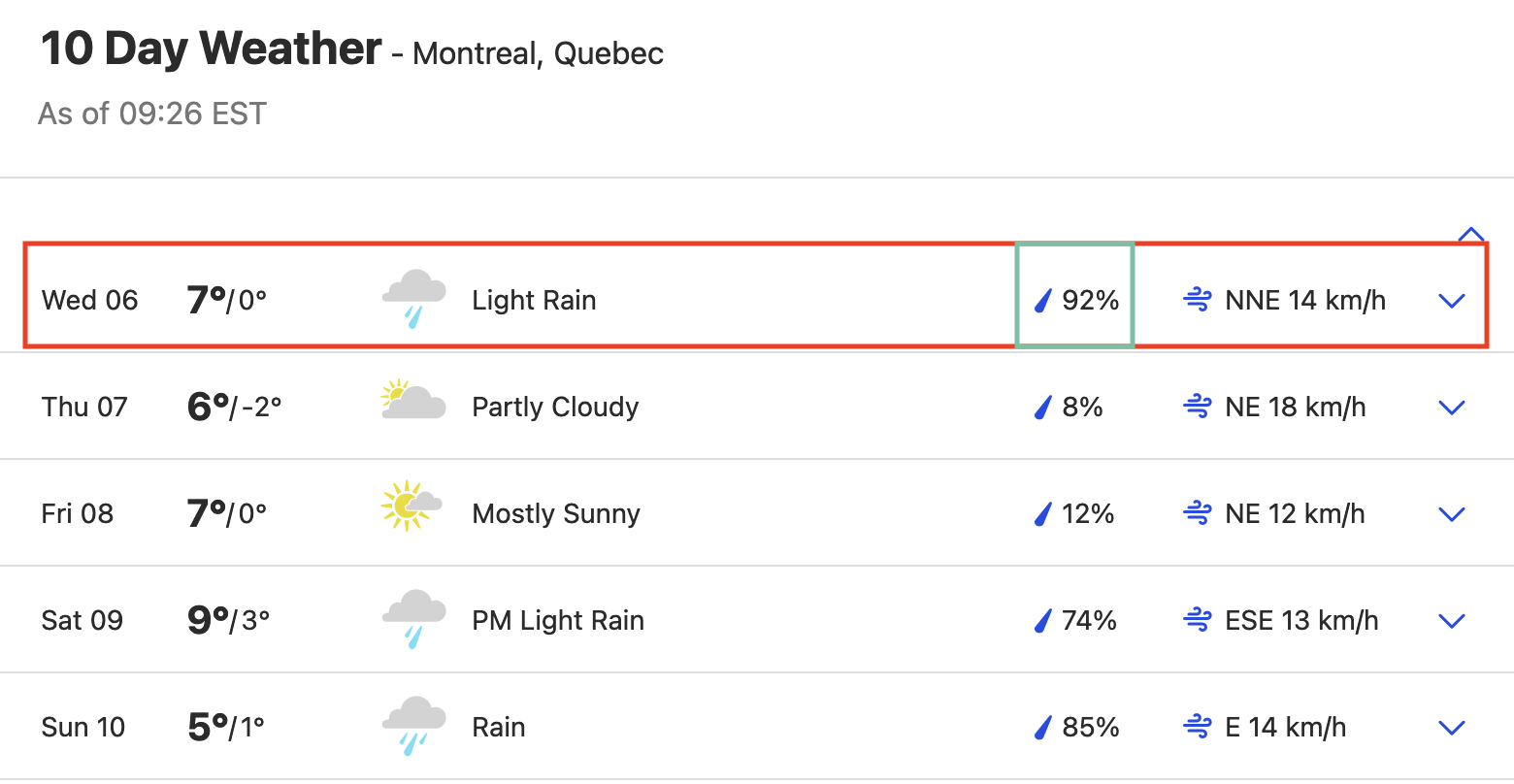
Intuition: Weather Forecasts

There is a 30% chance of rain tomorrow.
Dawid (1982)

Figure 1: Weather Forecasts on Tuesday, March 2024. Source: The Weather Chanel.

Consider a sequence of weather forecasts $\hat{s}(\mathbf{x}_t)$, where $t=1,\ldots, T$ denotes the days of forecast and $\mathbf{x}$ represents characteristics used in forecasting.

Intuition: Weather Forecasts

Within this sequence, we focus on days where $\hat{s}(\mathbf{x}_i)$ closely approximates 30%.

By assuming an infinite sequence, we can determine the long-term proportion $p$ of days where the forecasted event actually occurred.

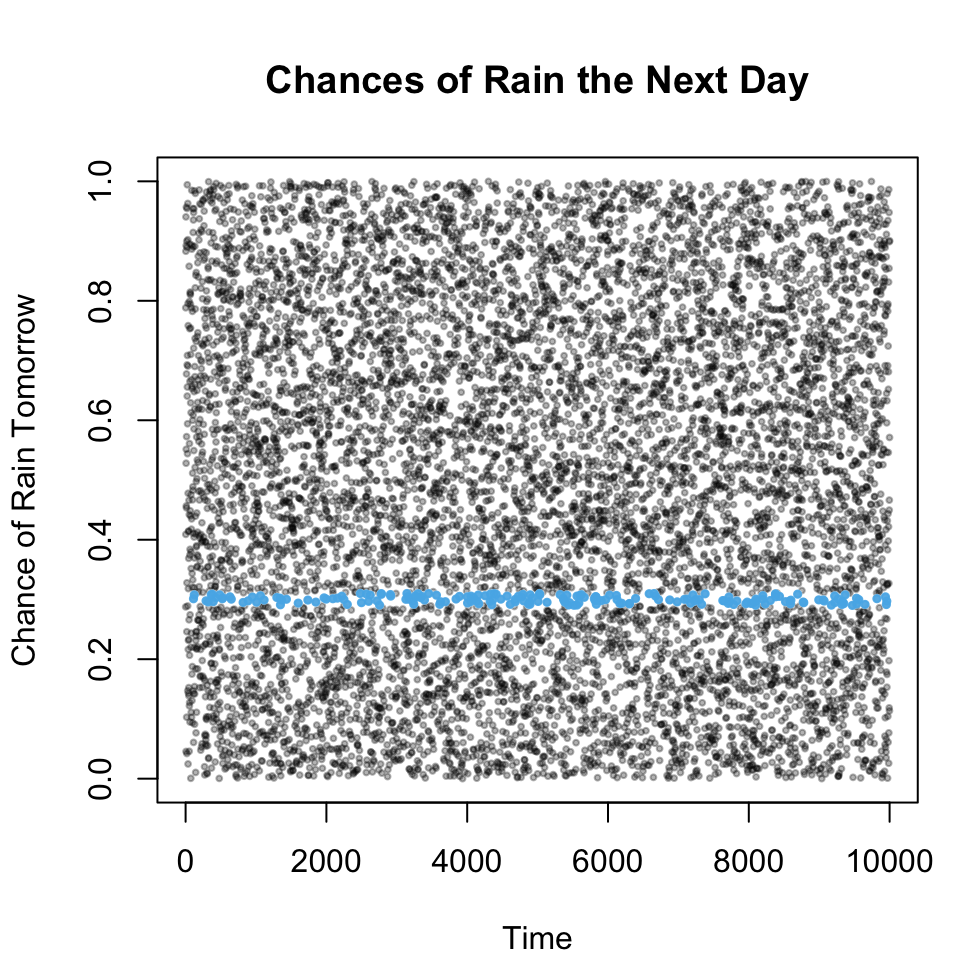
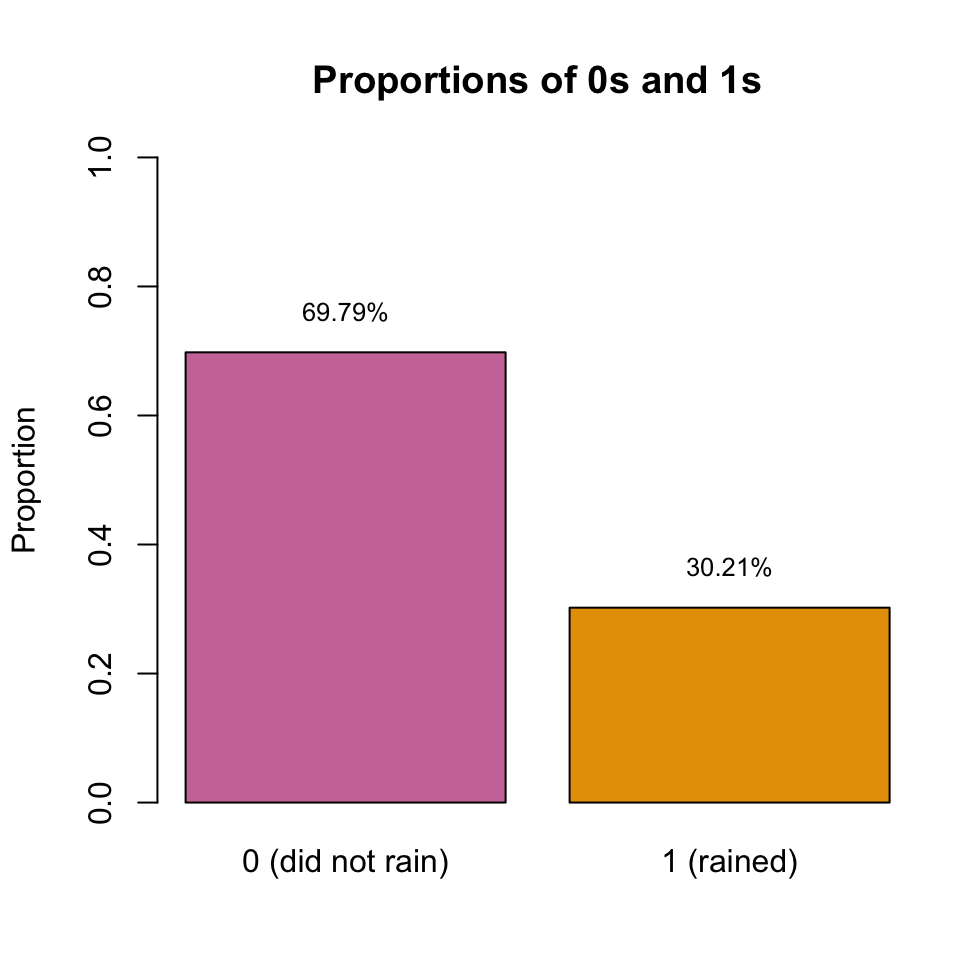
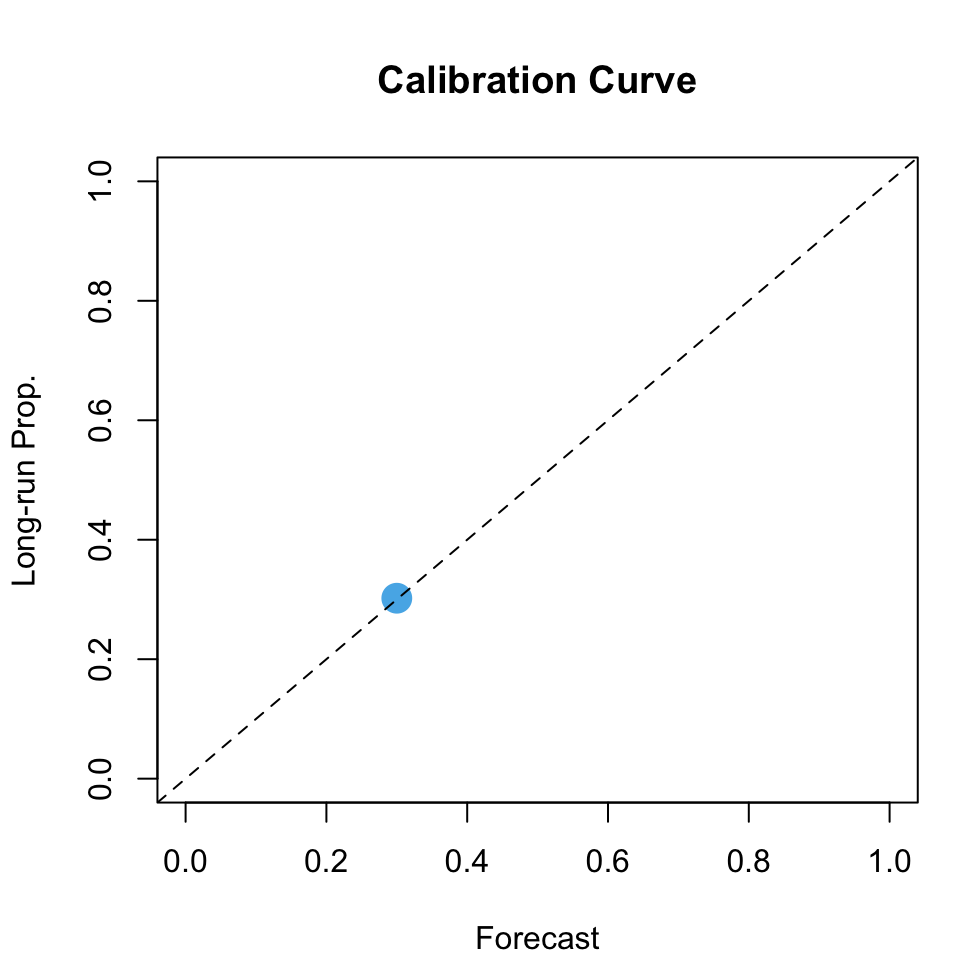
Intuition: Weather Forecasts

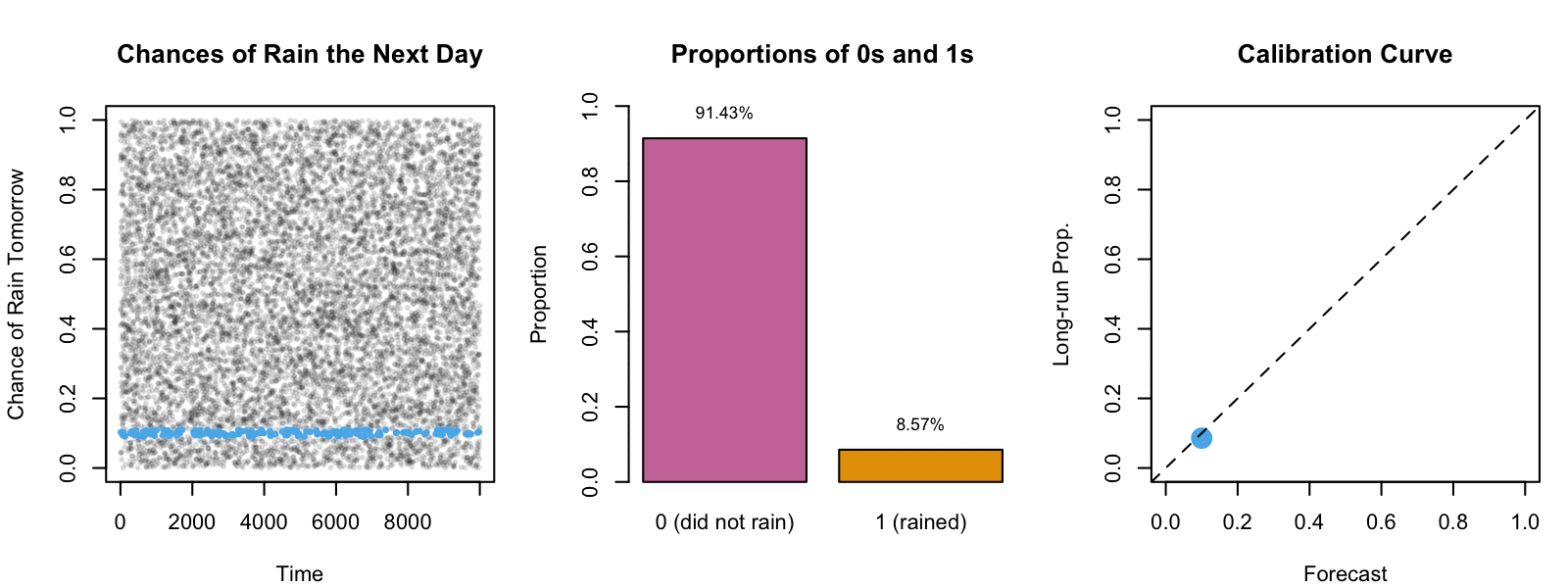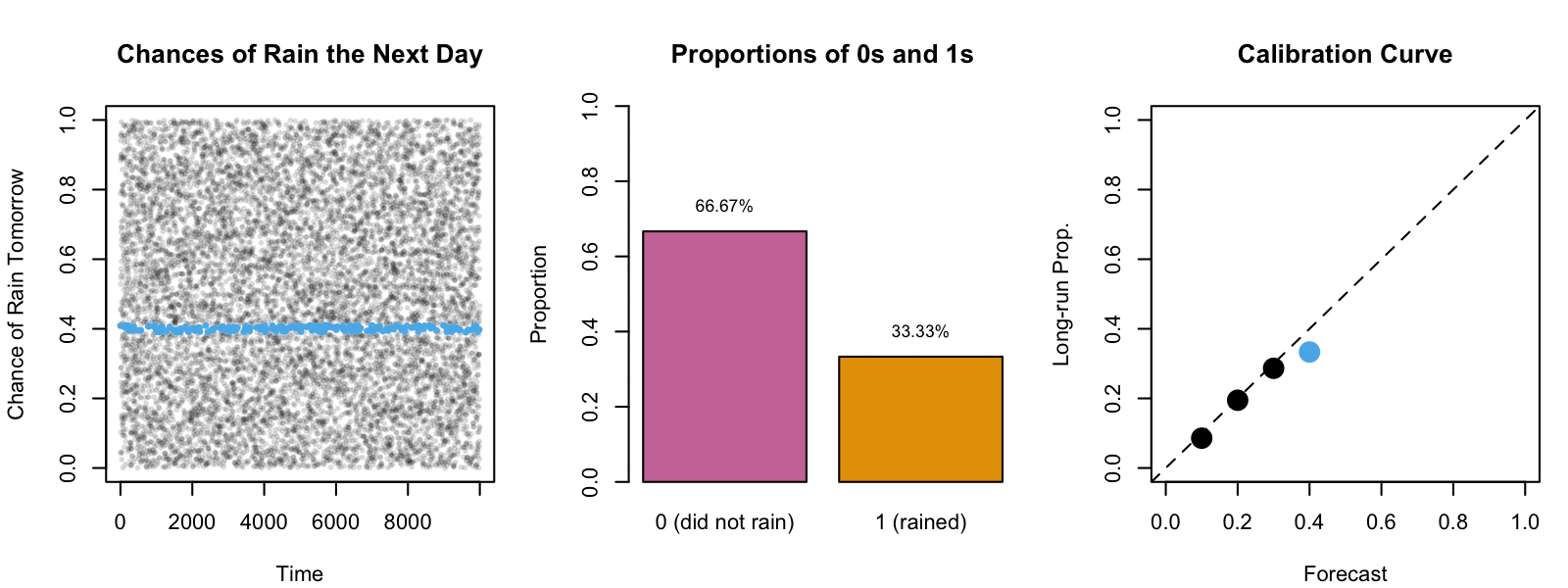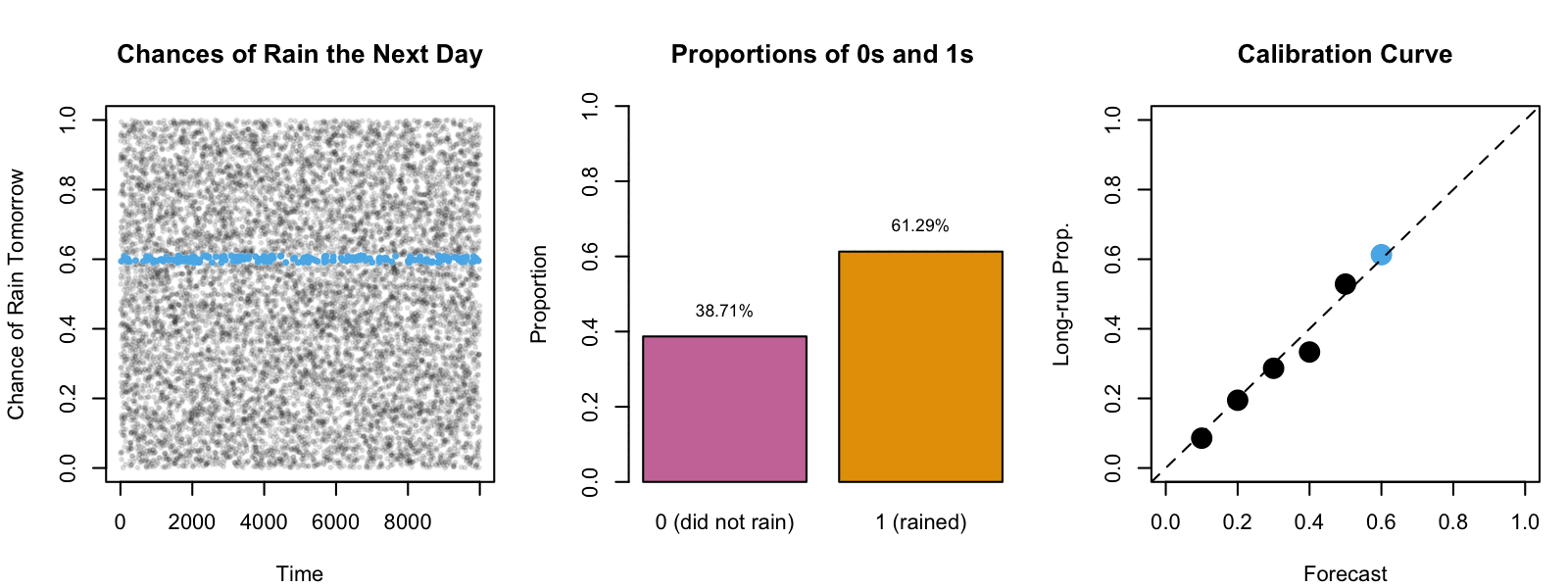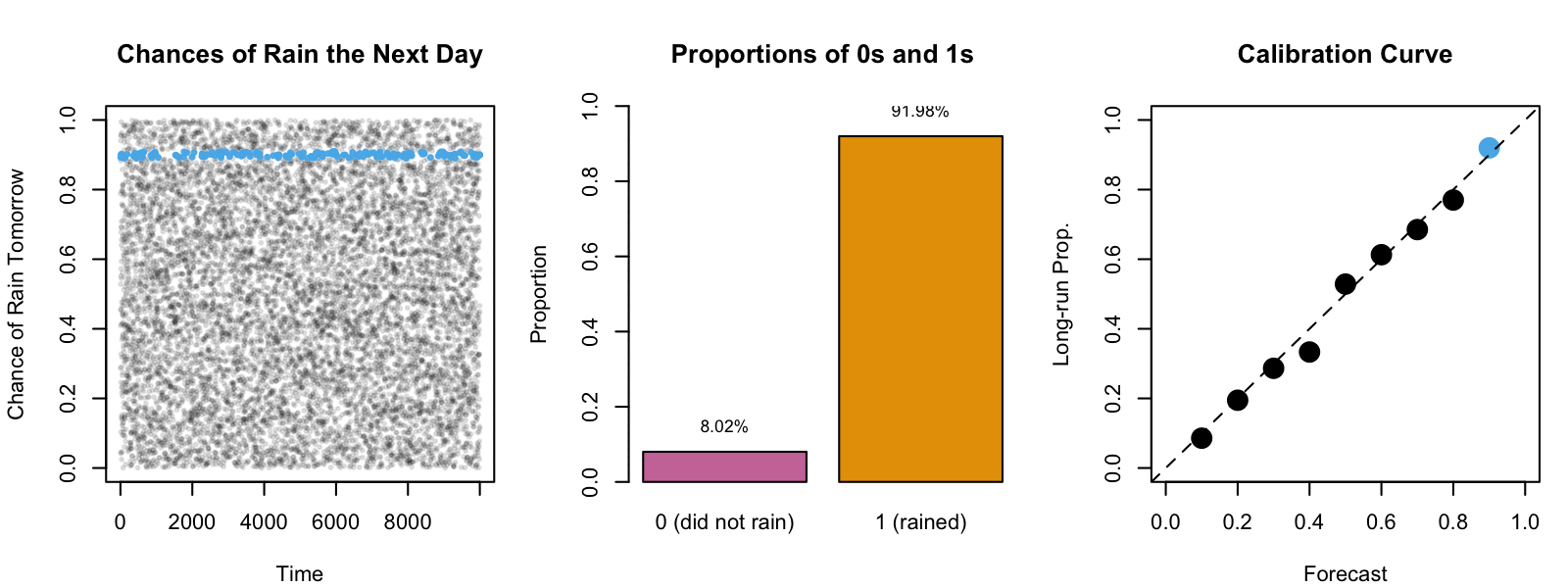
Figure 2: Example: Calibration of Weather Forecasts

Classification: Discriminatory Performances

In the example of the rain, we are interested in being able to discriminate between rainy/not rainy days.

What if we are also interested in the underlying risk?

For example, to assess whether:

a patient has a disease or not (Calster et al., 2019)
an insured will have an accident within the next year?

Second Example: Car Insurance

Driver A

Driver B

Probability of an accident

$p_A = 0.3$

$p_B = 0.7$

Annual Risk

$c_A = \$1,000$

$c_B = \$1,000$

The expected annual loss is therefore:

\[\mathbb{E}[S] = p_A c_A + p_B c_B = \$1,000\]

If the premiums are based on the accident probabilities, we then have:

Premium

$\pi_A = \$300$

$\pi_B = \$700$

Second Example: Car Insurance

But in practice, we do not observe the accident probabilities. Those are inferred.

If the model is not well calibrated, the premiums will lead to unfair pricing.

Driver A

Driver B

True Prob.

$p_A = 0.3$

$p_B = 0.7$

Estimated prob.
Premium

$\hat{s}(\mathbf{x}_A) = 0.4$
$\pi_A = \$400$

$\hat{s}(\mathbf{x}_B) = 0.6$
$\pi_B = \$600$

Estimated prob.
Premium

$\hat{s}(\mathbf{x}_A) = 0.1$
$\pi_A = \$100$

$\hat{s}(\mathbf{x}_B) = 0.9$
$\pi_B = \$900$

Estimated prob.
Premium

$\hat{s}(\mathbf{x}_A) = 0.2$
$\pi_A = \$200$

$\hat{s}(\mathbf{x}_B) = 0.4$
$\pi_B = \$400$

Repeated Observations

Unlike weather forecasting, it is harder to track indidivuals over time for an insurance company:

characteristics change over time (experience, age, exposition, …)
policyholders can switch to another insurance company at the end of their contract instead of renewing it.

The same applies in a medical context: we may not have repeated observations for the same patient.

Solution: observing a lot of individuals with similar characteristics.

After estimating individual probabilities, we group individuals accordingly and verify if the proportion of occurred events aligns with the estimated probability.

If the model is not calibrated, there exists ways to recalibrate it.

Calibration And Non Binary Variable

Calibration is not restricted to binary classifier.

In traditional regression, a model output denoted as $\hat{Z}$ is considered well-calibrated for a real-valued variable $Z$ when (Krüger and Ziegel, 2020): \[ \mathbb{E}\left[ Z \mid \hat{Z} \right] = \hat{Z}\enspace. \]

In Machado et al. (2024), we also explore the case of a multiclass variable.

When the target variable is binary, things become more complex as the predicted scores cannot be directly compared to the observed event.

Outline

What the remainder of the talk is about:

Reviewing of ways to measure and visualize calibration for a binary classifier.
Proposing a new metric based on local regression: the Local Calibration Score.
Observing the impact of a poor calibration on standard performance metrics.
Examining calibration for tree-based methods.

2 Calibration

Formal Notations

Let us consider a binary event $D$ whose observations are denoted $d_i=1$ if the event occurs, and $d_i=0$ otherwise, where $i$ denotes the $i$th observations.

Let us further assume that the probability of the event $d_i=1$ depends on individual characteristics:

\[p_i = s(\mathbf{x}_i)\]

where, with sample size $n > 0$, $i=1,\ldots, n$ represents individuals, and $\mathbf{x}_i$ the characteristics.

Predicting Risks

To estimate this probability, we can use a statistical model (e.g., a GLM) or a machine learning model (e.g., a random forest).

These models estimate a score ${\color{wongLightBlue}\hat{s}(\mathbf{x}_i)} \in [0,1]$, allowing the classification of observations based on the estimated probability of the event.

By setting a probability threshold $\tau$ in $[0, 1]$, one can predict the class of each observation: 1 if the event occurs, and 0 otherwise:

\[{\color{wongOrange}\hat{d}_i} = \begin{cases}1, & \text{if } {\color{wongLightBlue}\hat{s}(\mathbf{x}_i)} \geq \tau\\ 0, & \text{if } {\color{wongLightBlue}\hat{s}(\mathbf{x}_i)} < \tau\end{cases}\enspace.\]

However, to interpret the score as a probability, it is crucial that the model is well calibrated.

Definition

Calibration of a Binary Classifier (Schervish, 1989)

For a binary variable $D$, a model is well-calibrated when \[\begin{equation} \mathbb{E}[D \mid {\color{wongLightBlue}\hat{s}(\mathbf{X})} = p] = p, \quad \forall p \in [0,1]\enspace.\label{eq-calib-E} \end{equation}\]

Note: conditioning by $\{\hat{s}(\mathbf{x})=p\}$ leads to the concept of (local) calibration; however, as discussed by Bai et al. (2021), $\{\hat{s}(\mathbf{x})=p\}$ is a.s. a null mass event. Thus, calibration should be understood in the sense that \[ \mathbb{E}[D \mid \hat{s}(\mathbf{X}) = p]\overset{a.s.}{\to} p\text{ when }n\to\infty\enspace, \] meaning that, asymptotically, the model is well-calibrated, or locally well-calibrated in $p$, for any $p$.

2.1 Measuring Calibration

Measuring Calibration

To measure calibration, the literature provides:

visual approaches
metrics.

Usually, both are based on groups of observations, bins, defined using empirical quantiles of the estimated scores.

Calibration Curve

As previously illustrated with the example of weather forecast, one can plot a calibration curve to visualize the calibration of a model.

It involves estimating the function $\g(\cdot)$ that measures miscalibration on its predicted scores $\color{wongLightBlue}\hat{s}(\mathbf{x})$: \[ \g : \begin{cases} [0,1] \rightarrow [0,1]\\ p \mapsto \g(p) := \mathbb{E}[D \mid {\color{wongLightBlue}\hat{s}(\mathbf{x})} = p] \end{cases}\enspace. \tag{1}\]

The $\g$ function for a well-calibrated model is the identity function $\g(p) = p$.

Creating Bins

Challenge: having enough observations with identical scores is difficult.

Solution: grouping observations into $B$ bins, defined by the empirical quantiles of predicted scores $\color{wongLightBlue}\hat{s}(\mathbf{x})$.

The average of observed values ($\bar{d}_b$ with $b\in \{1, \ldots, B\}$), in each bin $b$ can then be compared with the central value of the bin.
A calibration curve (or reliability diagram (Wilks, 1990)) can be constructed by plotting the centers of each bin on the x-axis and the averages of corresponding observations on the y-axis.
When the model is well-calibrated, all $B$ points lie on the bisector.

Expected Calibration Error

Expected Calibration Error (ECE) (Pakdaman Naeini et al., 2015)

\[ \text{ECE} = \sum_{b=1}^{B} \frac{n_b}{n} \mid {\color{wongGold}\text{acc}(b)} - {\color{wongGreen}\text{conf}(b)} \mid \tag{2}\]

where $n$ is the sample size, $n_b$ is the number of observations in bin $b\in\{1, \ldots, B\}$.

In each bin $b$ associated with $\mathcal{I}_b$ containing the indices of instances within that bin:

The accuracy $\color{wongGold}\text{acc}(b)$, which measures the average of empirical probabilities or fractions of correctly predicted classes

\[ {\color{wongGold}\text{acc}(b)} = \frac{1}{n_b} \sum_{i \in \mathcal{I}_b} \mathbb{1}_{{\color{wongOrange}\hat{d}_i} = d_i} \]

The predicted class $\color{wongOrange}\hat{d}_i$ for observation $i$ is determined based on a classification threshold $\tau\in [0,1]$ where $\hat{d}_i = 1$ if ${\color{wongLightBlue}\hat{s}(\mathbf{x}_i)} \geq \tau$ and $0$ otherwise

The Confidence $\color{wongGreen}\text{conf}(b)$, indicating the model’s average confidence within bin $b$ by averaging predicted scores.

\[ {\color{wongGreen}\text{conf}(b)} = \frac{1}{n_b} \sum_{i \in \mathcal{I}_b} {\color{wongLightBlue}\hat{s}(\mathbf{x}_i)} \]

Brier Score, MSE

Another metric, the Brier Score, does not depend on bins.

Brier Score (Brier, 1950)

\[ BS = \frac {1}{n} \sum_{i=1}^{n} (d_i - {\color{wongLightBlue}\hat{s}(\mathbf{x}_i)})^2 \tag{3}\]

where $d_i$ is the observed event and $\color{wongLightBlue}\hat{s}(\mathbf{x}_i)$ the estimated score.

MSE

By substituting the observed event $d_i$ by the true probability $p_i$ (which can only be observed in an experimental setup), the metrics becomes the MSE:

\[ \text{True MSE} = \frac{1}{n} \sum_{i=1}^{n} (p_i - {\color{wongLightBlue}\hat{s}(\mathbf{x}_i)})^2 \tag{4}\]

Smoother Visualization Technique

We propose an alternative approach to visualize model calibration, aiming for a smoother representation than that provided by the method based on quantiles: local regression (Loader, 1999)

Measuring calibration consists in estimating a conditional expectation: a local regression seems appropriate.
Local Regression have been disregarded in high dimensions due to poor properties, but it is highly efficient in small dimensions, as in this case with only one predictive feature, $\color{wongLightBlue}\hat{s}(\boldsymbol{x}) \in [0,1]$.
Given the number of data points, the precision of quantile binning can be sub optimal when determining the appropriate bin count.
By contrast, with local regression, one can specify the percentage of nearest neighbors, providing greater flexibility.

Local Regression

The degree of the polynomial determines the construction of the polynomial regression.

library(locfit)
locfit_0 <- locfit(
    formula = d ~ lp(scores, nn = 0.15, deg = 0), 
    kern = "rect", maxk = 200, 
    data = tibble(
      d = observed_events,
      scores = scores
    )
  )

Local Regression

The degree of the polynomial determines the construction of the polynomial regression.

library(locfit)
locfit_0 <- locfit(
    formula = d ~ lp(scores, nn = 0.15, deg = 0), 
    kern = "rect", maxk = 200, 
    data = tibble(
      d = observed_events,
      scores = scores
    )
  )
linspace <- seq(0, 1, length.out = 100)
locfit_linspace <- predict(locfit_0, newdata = linspace)

We employ the trained model to make predictions on a linear space with values in $[0, 1]$: this provides a continuous calibration profile, based on uniformly distributed points to evaluate $\g$.

Our New Metric: LCS

Local Calibration Score (LCS)

A local regression of degree 0, denoted as $\hat{\g}$, is fitted to the predicted scores $\color{wongLightBlue}\hat{s}(\mathbf{x})$.

This fit is then applied to a vector of linearly spaced values within the interval $[0,1]$.

Each of these points is denoted by $\color{wongPurple}l_j$, where $j \in \{1, \ldots, J\}$, with $J$ being the target number of points on the visualization curve.

The LCS is defined as: \[ \text{LCS} = \sum_{j=1}^{J}w_j \big(\hat{\g}({\color{wongPurple}l_j}) - {\color{wongPurple}l_j}\big)^2\enspace, \tag{5}\] where $w_j$ is a weight defined as the density of the score at $\color{wongPurple}l_j$.

Local Regression: Issue

The local regression model relies on neighboring points to make predictions.

Challenge: Problems at the edges when the range of predicted scores $\color{wongLightBlue}\hat{s}(\mathbf{x})$ does not cover the entire interval $[0,1]$.

In such cases, predicted values beyond this range may deviate from the bisector, leading to a misinterpretation of calibration.

Solution: we adjust the linear space used for predictions by the local regression model to align with the full range of observed scores $\hat{s}(\mathbf{x})$.

3 Impact of a Poor Calibration

Data Generating Process

We simulate binary observations as in Gutman et al. (2022):

\[D_i \sim \mathcal{B}(p_i),\] where individual prob. are obtained using a logistic sigmoid function:

\[p_i = \frac{1}{1+\exp(-\eta_i)},\] \[\eta_i = \mathbf{a} \mathbf{x}_i + \varepsilon_i\] with $\mathbf{a} = \begin{bmatrix}a_1 & a_2 & a_3 & a_4\end{bmatrix} = \begin{bmatrix}0.1 & 0.05 & 0.2 & -0.05\end{bmatrix}$ and $\mathbf{x}_i = \begin{bmatrix}x_{1,i} & x_{2,i} & x_{3,i} & x_{4,i}\end{bmatrix}^\top$.

The observations $\mathbf{x}_i$ are drawn from a $\mathcal{U}(0,1)$ and $\varepsilon_i \sim \mathcal{N}(0, 0.5^2)$.

The Use of the Logistic Setup

Logistic Regression is a.s. well calibrated

Consider a dataset $\{(d_i,\mathbf{x{_i}})\}$, where {$\mathbf{x}$} are $k$ features ($k$ being fixed), so that $D|\boldsymbol{X}=\mathbf{x} \sim \mathcal{B}\big(s(\mathbf{x})\big)$ where \[ s(\mathbf{x})=\frac{\exp[\beta_0+\mathbf{x}^\top\boldsymbol{\beta}]}{1+\exp[\beta_0+\mathbf{x}^\top\boldsymbol{\beta}]}. \] Let $\widehat{\beta}_0$ and $\widehat{\boldsymbol{\beta}}$ denote maximum likelihood estimators. Then, for any $\mathbf{x}$, the score defined as \[ \hat{s}(\mathbf{x})=\frac{\exp[\hat\beta_0+\mathbf{x}^\top\hat{\boldsymbol{\beta}}]}{1+\exp[\hat\beta_0+\mathbf{x}^\top\hat{\boldsymbol{\beta}}]} \] is well-calibrated in the sense that \[ \mathbb{E}[D \mid \hat{s}(\mathbf{x}) = p]\overset{a.s.}{\to} p\text{ as }n\to\infty. \]

Forcing Poor Calibration

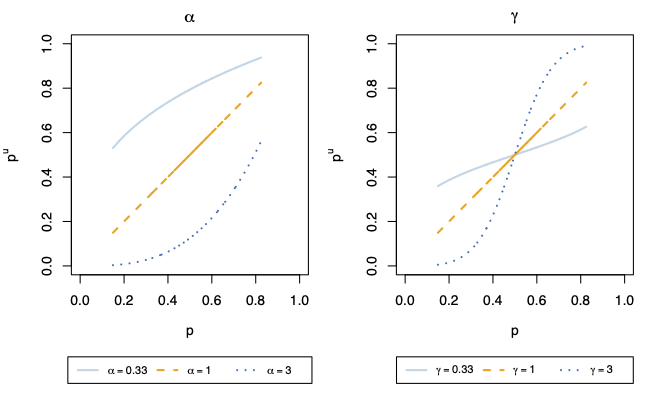
To simulate uncalibration, we generate samples of $2,000$ observations and we apply (monotonous) transformations to the true probabilities, either on:

the latent probability $p_i$:
\[p_i^{u} = \left(\frac{1}{1+\exp(-\eta_i)}\right)^{\color{wongPurple}\alpha}\enspace. \tag{6}\]
the linear predictor $\eta_i$:
\[ \eta_i^u = {\color{wongPurple}\gamma} \times \left((-0.1)x_1 + 0.05x_2 + 0.2x_3 - 0.05x_4 + \varepsilon_i\right)\enspace . \tag{7}\]

The resulting transformed probabilities are considered as the scores: ${\color{wongLightBlue}\hat{s}(\mathbf{x})} := \color{wongLightBlue}p_i^u$

Distortions

We examine variations in $\{1/3, 1, 3\}$ for $\alpha$ and $\gamma$
For each of the 6 scenarios, we generate 200 samples of $2,000$ obs.

Figure 3: Distorted Prob. as a Function of True Prob., Depending on the Value of $\alpha$ (left) or $\gamma$ (right).

Impacts: Calibration Metrics

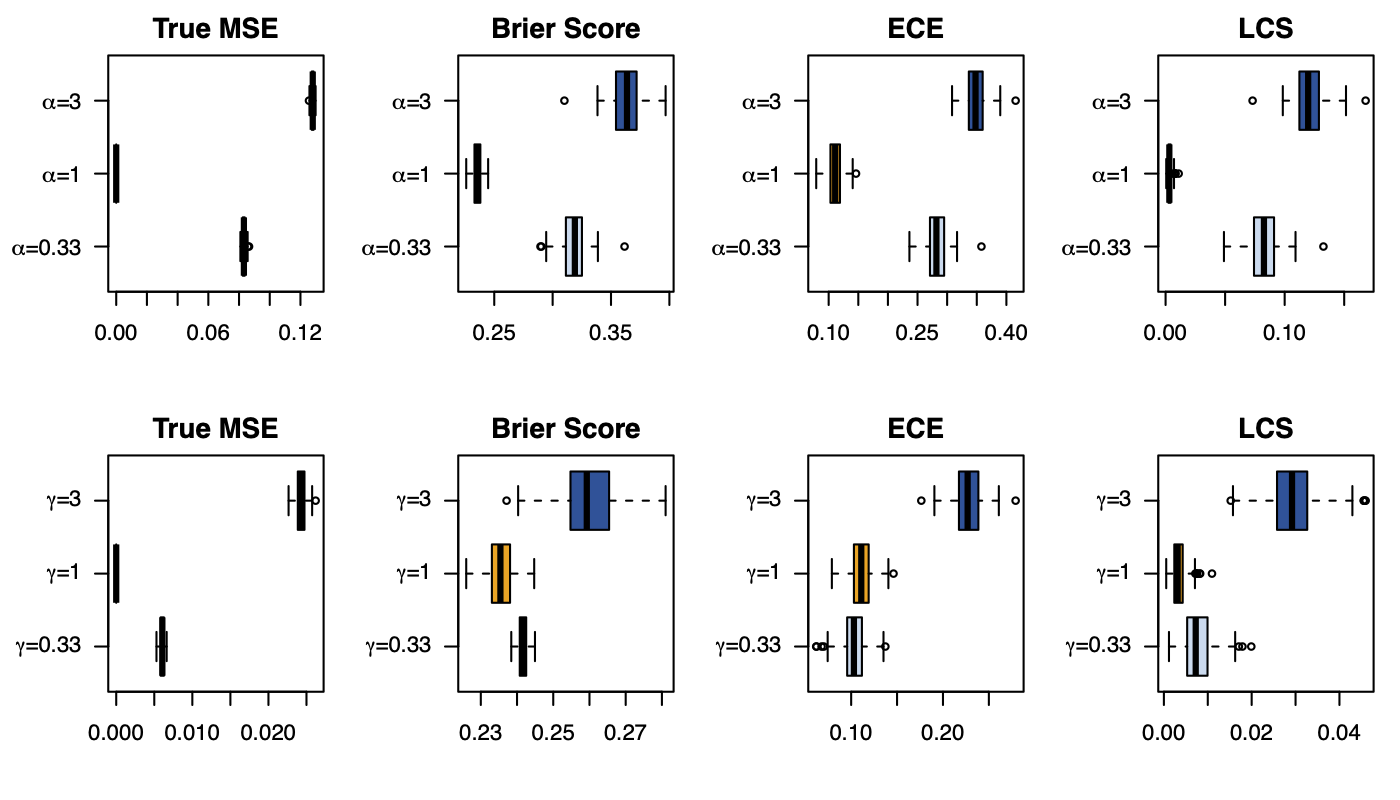
Figure 4: Calibration Metrics on 200 Simulations for each Value of $\alpha$ (top) or $\gamma$ (bottom).

Impacts: Calibration Curves

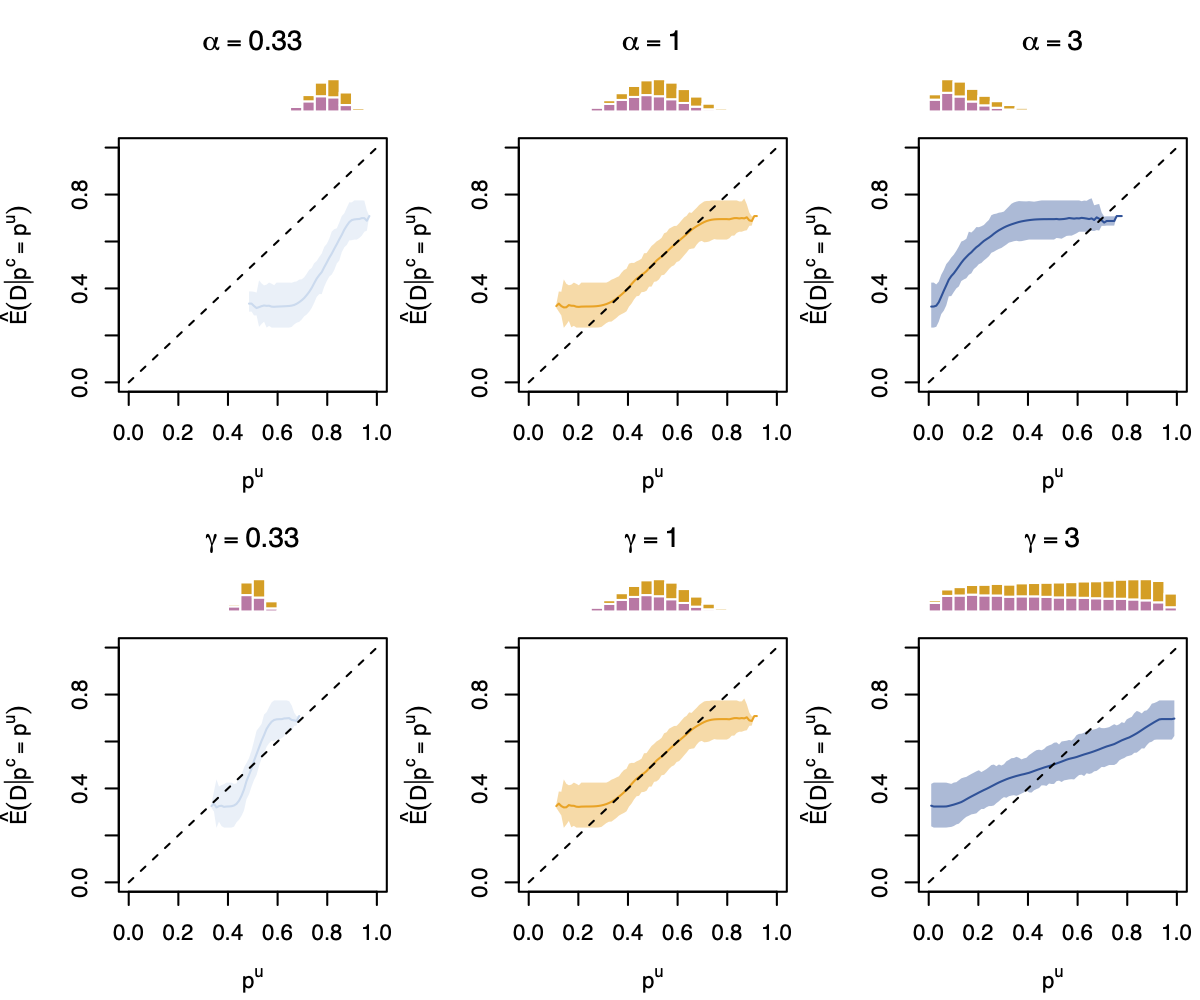
Figure 5: Calibration Curve Obtained with Local Regression, on 200 simulations for each Value of $\alpha$ (top) or $\gamma$ (bottom). Distribution of the true probabilities are shown in the histograms (gold for $d=1$, purple for $d=0$).

(Mis-)Calibration and standard metrics

What are the impacts of miscalibration on standard metrics?

We will consider metrics based on the predictive performances calculated using a confusion table:

Table 2: Confusion Table
Actual/Predicted	Positive	Negative
Positive	TP	FN
Negative	FP	TN

\[\text{TPR} = \frac{\text{TP}}{\text{TP} + \text{FN}}; \quad \text{FPR} = \frac{\text{FP}}{\text{FP} + \text{TN}}\]

(Mis-)Calibration and standard metrics

\[\text{Accuracy} = \frac{\text{TP} + \text{TN}}{\text{N}}\]

Overall correctness of the model

\[\text{Sensitivity} = \frac{\text{TP}}{\text{TP} + \text{FN}}\]

Ability to correctly identify positive class

\[\text{Specificity} = TPR = \frac{\text{TN}}{\text{TN} + \text{FP}}\]

Ability to correctly identify negative class

AUC (Area Under Curve)

TPR and TFP for various prob. threshold $\tau$

(Mis-)Calibration and standard metrics

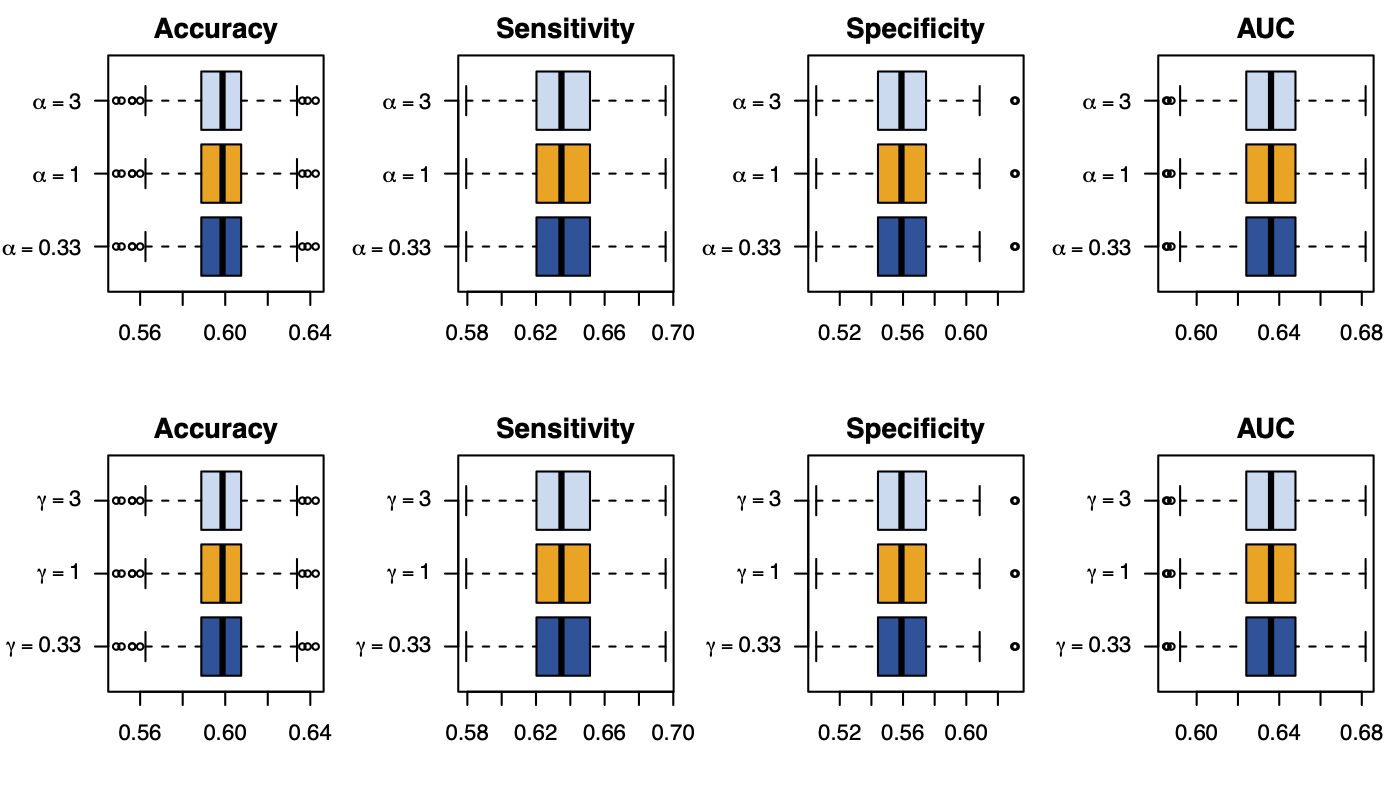
Figure 6: Standard Goodness of Fit Metrics on 200 Simulations for each Value of $\alpha$ (top) or $\gamma$ (bottom). The probability threshold is set to $\tau=0.5$.

4 Recalibration

Recalibration

When a binary classifier is not calibrated, the literature advocates recalibrating the model.

The basic idea is to apply a transformation to the scores, e.g.:

Platt Scaling (Platt et al., 1999)
Isotonic Regression (Zadrozny and Elkan, 2002)
Beta Calibration (Kull, Silva Filho, et al., 2017)

We suggest considering local regression too.

Methodology

To recalibrate a model, we adopt the following methodology:

split the dataset into three sets: train, calibration, test
train a classifier on a train set
apply a recalibration technique on the predicted scores from the calibration set
examine performances and calibration on the test set.

Platt Scaling

Platt scaling (Platt et al., 1999) was initially introduced for SVM.

The method consists in applying a logistic regression to the scores predicted on the calibration set to learn $a$ and $b$: \[ \g\big(\hat{s}(\mathbf{x})\big) = \frac{1}{1+\exp{\left\{-\big(a\hat{s}(\mathbf{x})+b\big)\right\}}}\enspace \tag{8}\]

Caveat: if the model was already well calibrated, applying Platt scaling will make it uncalibrated, as the identity function is not a member of the logistic family.

Isotonic Regression

Isotonic regression (Zadrozny and Elkan, 2002) comes from a constrained optimization problem solved using the Pool-Adjacent-Violators Algorithm.

Using this algotithm, the predicted scores remain monotonic.

Find the isotonic (monotonically increasing) function $g(\cdot)$ that minimizes \[ \begin{array}{rrclcl} \displaystyle & \sum_{i=1}^n \left(d_{i} - g(\hat{s}(\mathbf{x}_i))\right)^2 \\ \textrm{s.t.} & g(\hat{s}(\mathbf{x}_1)) \leq \ldots \leq g(\hat{s}(\mathbf{x}_n)) \end{array}\enspace . \]

Caveat: predicted scores $\color{wongLightBlue}\hat{s}(\mathbf{x})$ are assumed to be well-ordered, limiting the ability of isotonic regression to correct non-monotonic probability distortions.

Beta Calibration

Instead of assuming normal distribution of scores within each class (0 and 1), with Beta calibration (Kull, Silva Filho, et al., 2017) the scores are assumed to follow a beta distribution.

Parameters $a$, $b$ and $c$ are estimated on a calibration set:

\[ \g\left(\hat{s}(\mathbf{x})\right) = \frac{1}{1+\exp{\left\{-c\right\}}\left(\frac{\hat{s}(\mathbf{x})^a}{(1-\hat{s}(\mathbf{x}))^b}\right)} \tag{9}\]

where conditioning $a, b \geq 0$ leads to an increasing map function.

Note: in contrast to Platt scaling, the Beta calibration family includes the identity function, allowing it to maintain score calibration when it is already calibrated.

Local Regression

Local regression can be used to recalibrate scores.

The idea is to fit a local regression of degree 0 to the predicted scores on a calibration set.

This allows to estimate $\hat{\mathbb{E}}[D \mid {\color{wongLightBlue}\hat{s}(\mathbf{X})} \in \mathcal{V}_p]$, where $p \in [0,1]$, where $\mathcal{V}_p$ represents the neighborhood of a given $p$, defined using a percentage of nearest neighbors among the set of evaluation points.

$\hat{\mathbb{E}}[D \mid {\color{wongLightBlue}\hat{s}(\mathbf{X})} \in \mathcal{V}_p]$ is an approximation the function $\g$.

Note: to improve smoothness particularly in regions with limited data points (e.g., when the predicted scores $\hat{s}(\mathbf{x})$ are close to 0 and 1), employing with polynomial degrees of 1 and 2 is an alternative worth considering.

Scores Recalibration

Reference: metric computed using the uncalibrated scores $\color{wongLightBlue}\hat{s}(\mathbf{x})$.

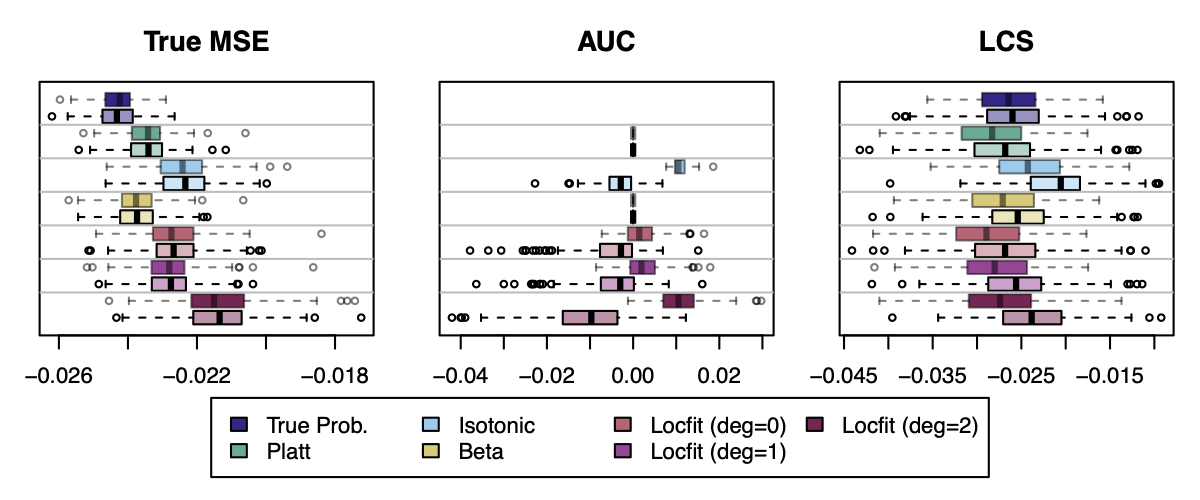
Figure 7: Metrics After Recalibration (for $\gamma=3$), on the Calibration (transparent colors) and on the Test Set (full colors).

5 Classification for Tree-Based Methods

Trees

Are trees well calibrated?

Some learning algorithms are designed to yield well-calibrated probabilities. These include decision trees, whose leaf probabilities are optimal on the training set
(Kull, Filho, et al., 2017)

Earlier studies show that also classical methods such as decision trees, boosting, SVMs and naive Bayes classifiers tend to be miscalibrated
(Wenger et al., 2020)

5.1 Illustrative Example: Regression Tree

Data Generating Process

We simulate binary observations in a simpler framework:

\[D_i \sim \mathcal{B}(p_i),\] where individual prob. are obtained using a logistic sigmoid function:

\[p_i = \frac{1}{1+\exp(-\eta_i)},\] \[ \eta_i = a_1 x_1 + a_2 x_2 - \frac{a_1+a_2}{2}\enspace \tag{10}\] with $\begin{bmatrix}a_1 & a_2\end{bmatrix} = \begin{bmatrix}4 & 3\end{bmatrix}$ and $x_1$ and $x_2$ are drawn from a $\mathcal{U}(0,1)$.

Data Generating Process

We generate 200,000 obs: 100,000 in train, 50,000 in calibration, and 50,000 in test.

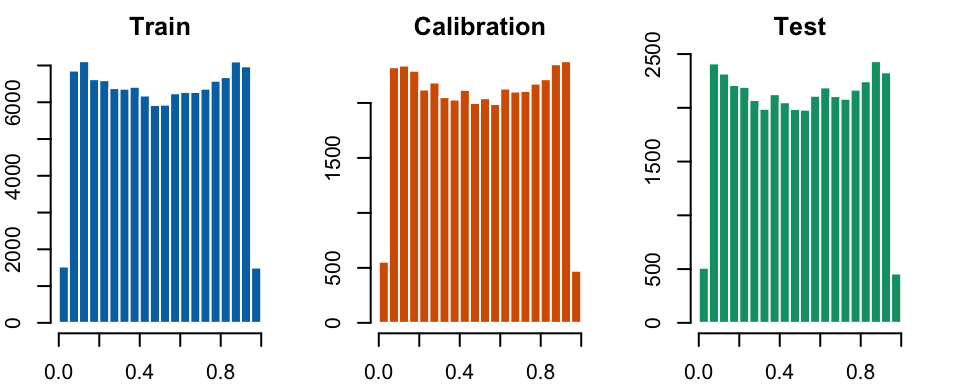
Figure 8: Distribution of the True Probabilities

Data Generating Process

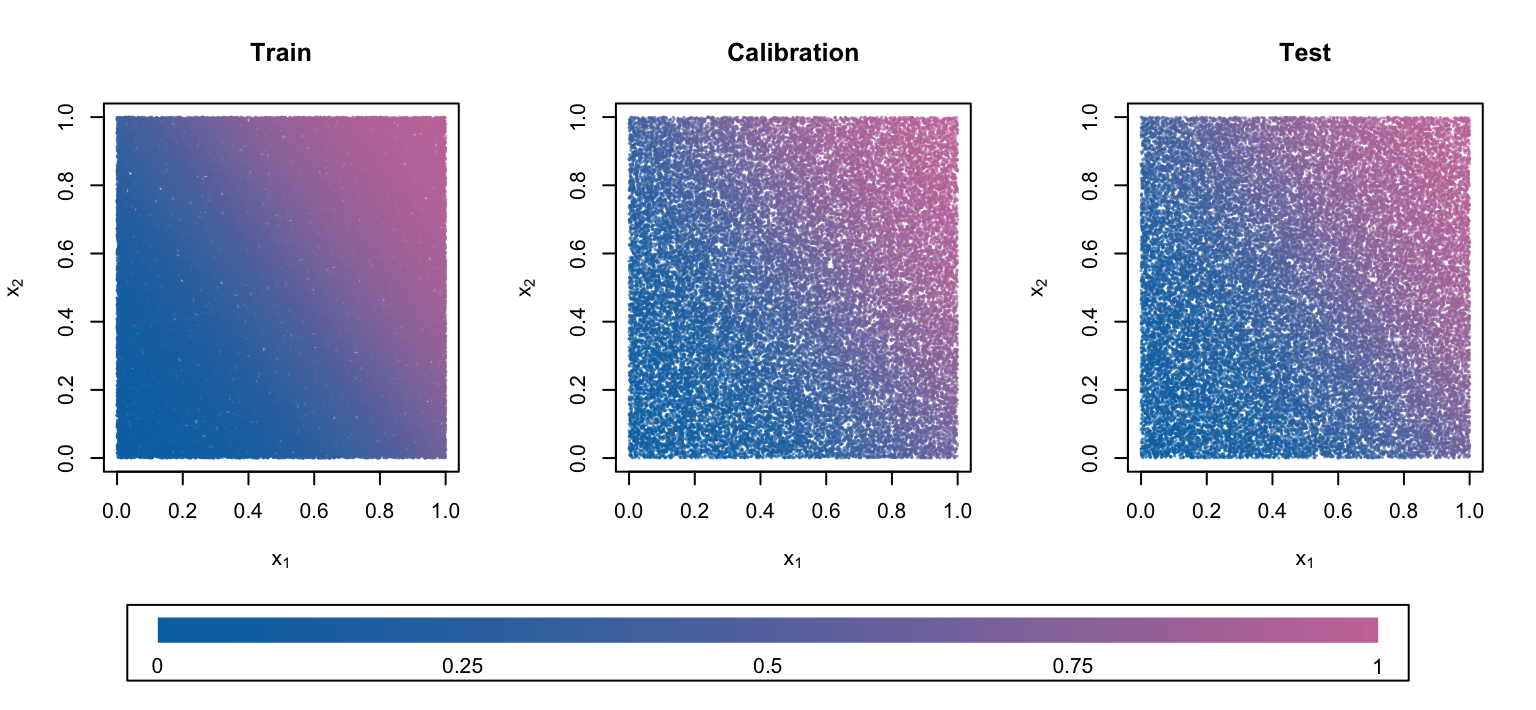
Figure 9: Drawn Probabilities $p_i$

Data Generating Process

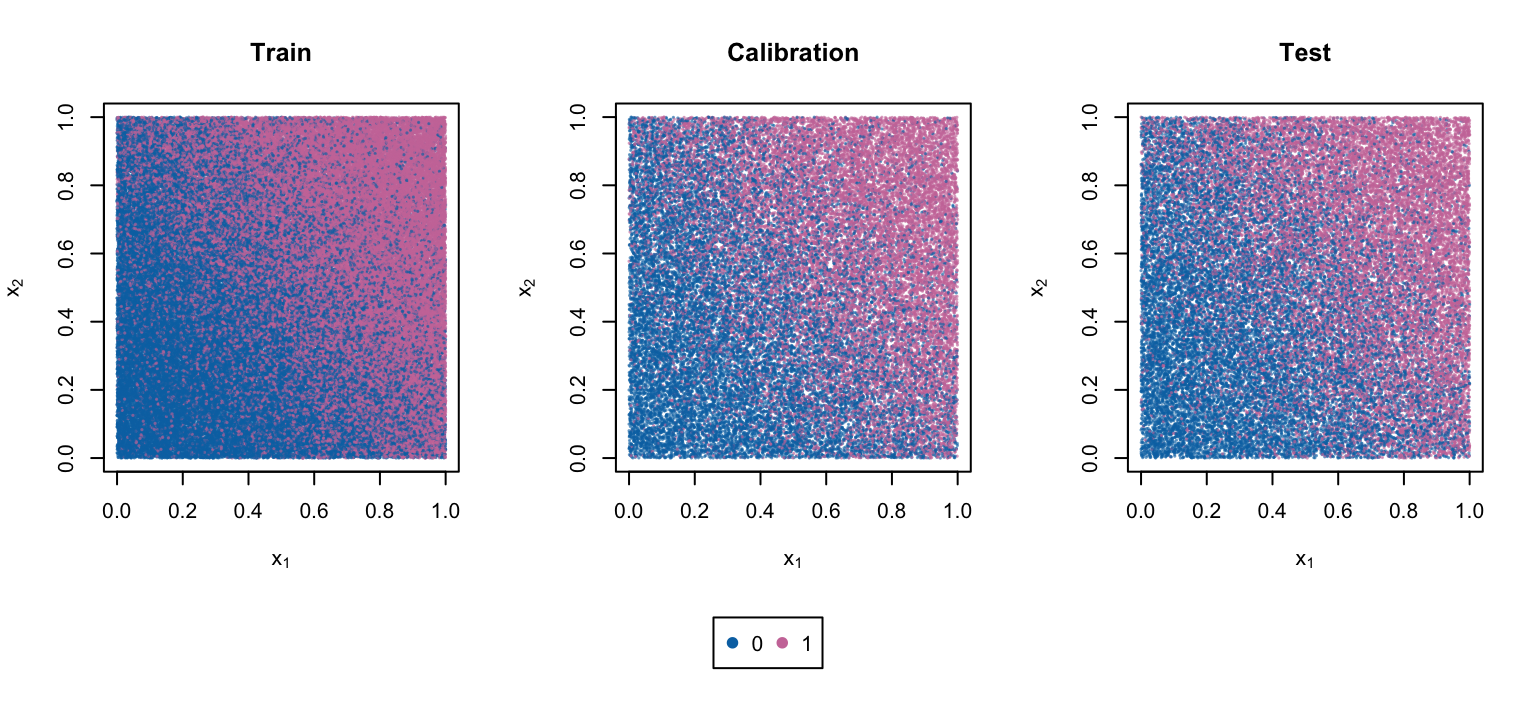
Figure 10: Observed Event $d_i$

Training a Regression Tree

We train a regression tree (Breiman, 1984), with a minimal number of cases in the terminal node equal to $1/10,000$ of the size of the train data, i.e., 12 observations.

The tree is pruned depending on the improvement made on the R-squared. The procedure is done by cross-validation.

For each terminal leaf of the tree, the average value of the observed events from the train set that fall into the leaf is computed: this is how the estimated scores are computed. For a terminal leaf node $\ell$: \[ \text{score}(\ell) = \frac{1}{N_\ell} \sum_{i \in \ell} d_i, \tag{11}\] where $N_\ell$ is the number of observations in terminal node $\ell$.

The predicted score $\color{wongLightBlue}\hat{s}(\mathbf{x}_i)$ is the value $\text{score}(\ell)$ of terminal leaf in which observation $i$ belongs.

Training a Regression Tree

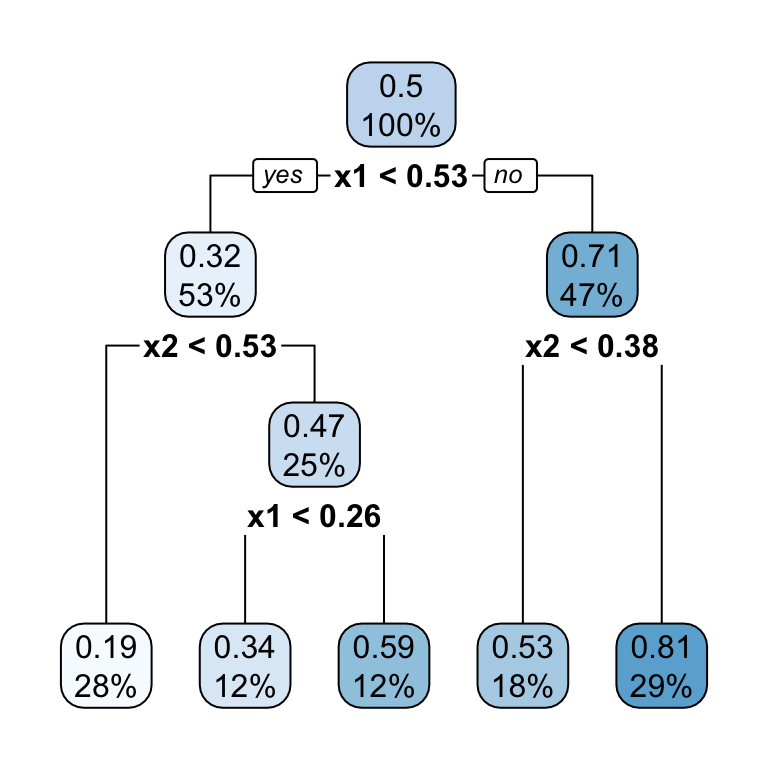
Figure 11: Decision Tree Estimated with `minbuckket = 12`. In each node, the value on top is the average of $d_i$ and the bottom value is the proportion of observations from the train sample.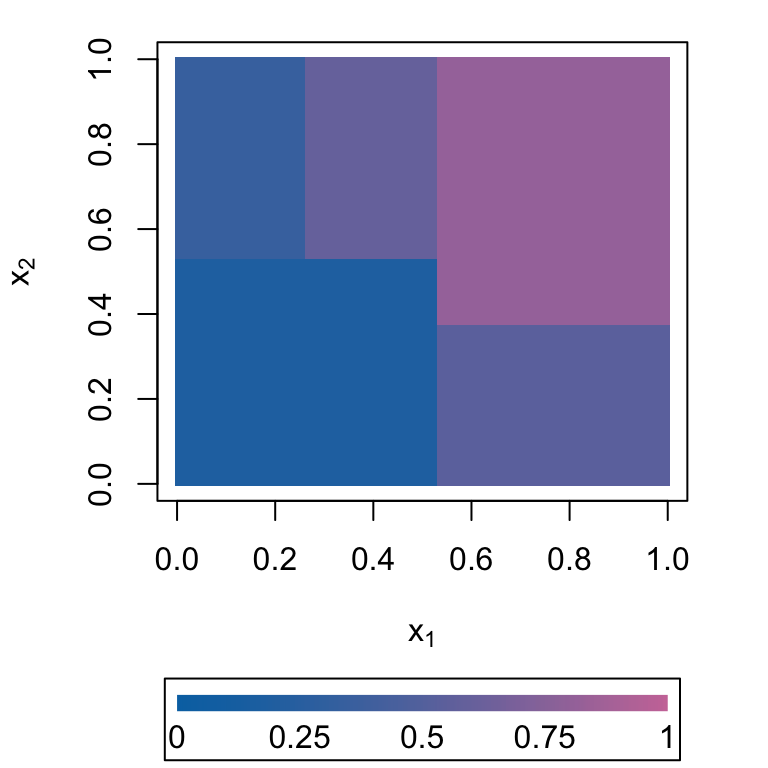

Figure 12: Predicted Scores $\hat{s}(\mathbf{x})$ on a Grid of Evenly Spaced Values

Calibration Curves

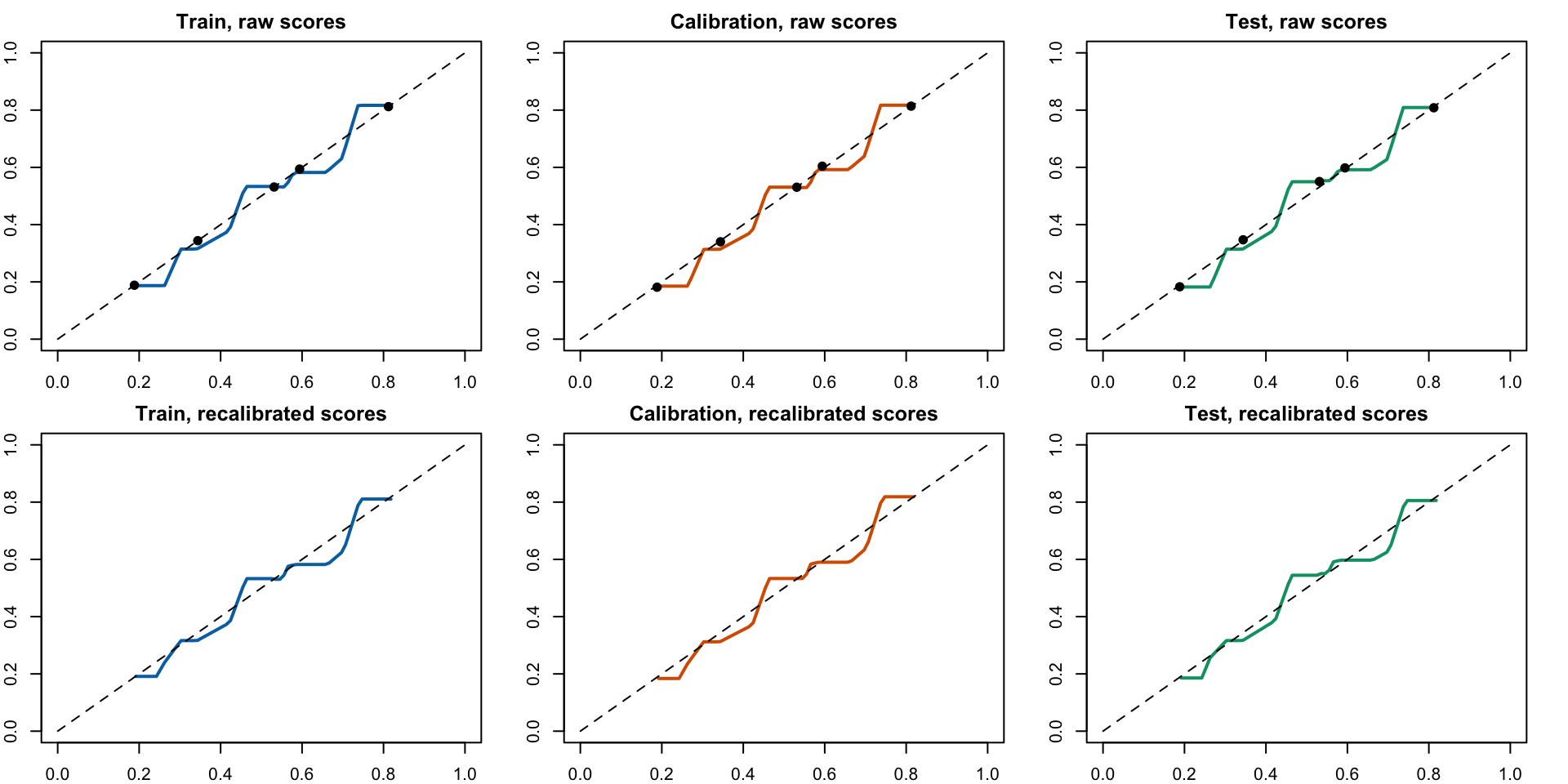
Figure 13: Calibration Curve with Uncalibrated Scores (top) and Recalibrated Scores (bottom)

MSE	Accuracy	AUC	Brier Score	LCS	Sample
True Probabilities
0.000	0.736	0.813	0.176	0.000	Train
0.000	0.741	0.818	0.174	0.000	Calibration
0.000	0.737	0.815	0.176	0.000	Test
No Calibration
0.014	0.716	0.774	0.190	0.001	Train
0.014	0.720	0.779	0.188	0.001	Calibration
0.014	0.720	0.775	0.189	0.002	Test

MSE	Accuracy	AUC	Brier Score	LCS	Sample
True Probabilities
0.000	0.736	0.813	0.176	0.000	Train
0.000	0.741	0.818	0.174	0.000	Calibration
0.000	0.737	0.815	0.176	0.000	Test
Local Reg (deg=0)
0.014	0.716	0.774	0.190	0.001	Train
0.014	0.720	0.779	0.188	0.001	Calibration
0.014	0.720	0.775	0.189	0.001	Test

Predicted Scores vs True Probabilities

Without Recalibration
After Recalibration

Figure 14: True Probabilities (top) and Predicted Scores (bottom)

Figure 15: True Probabilities (top) and Recalibrated Predicted Scores (bottom)

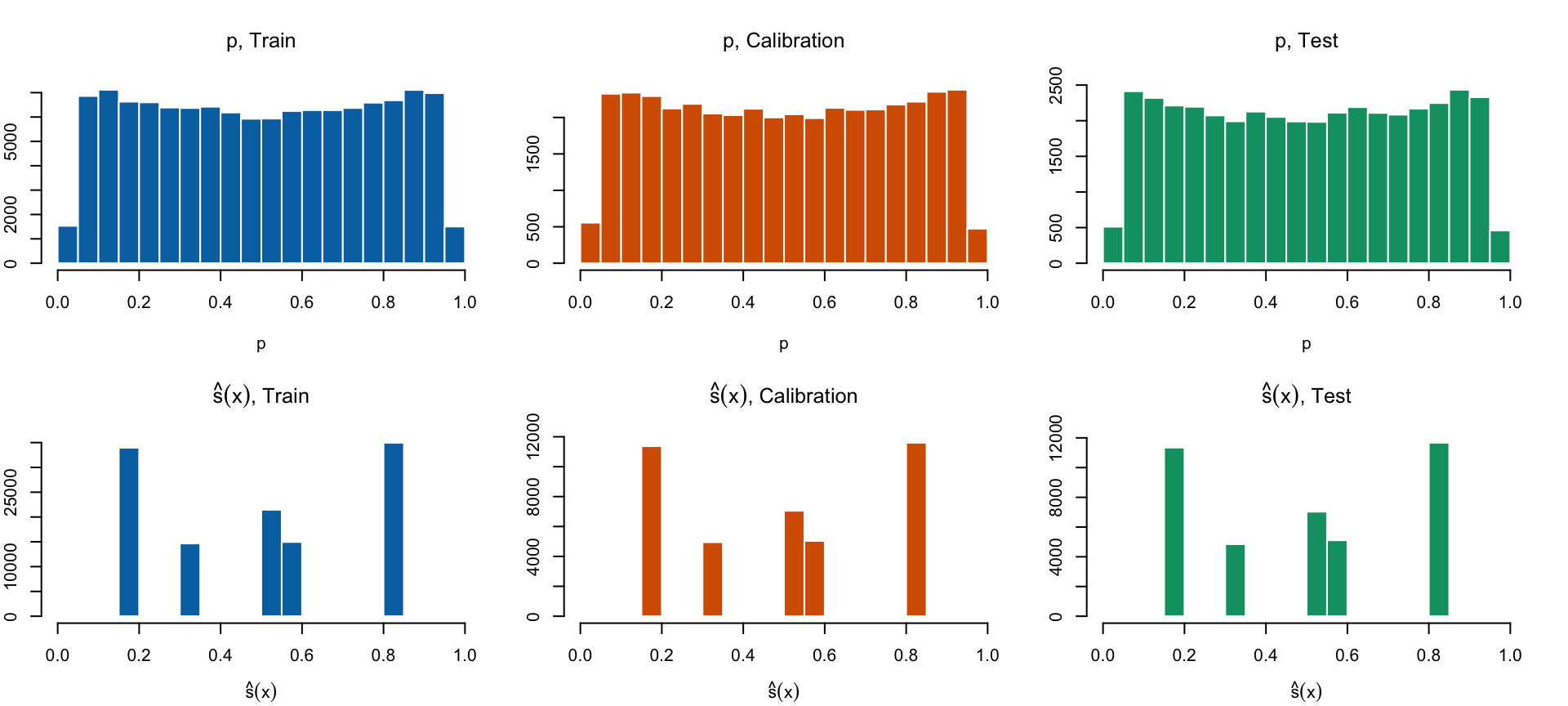
5.2 Relationship Between Tree Depth, Performances, and Calibration

Varying Tree Depth

Tree depth matters:

With a small tree with only two terminal leaves, there will be only two distinct predicted scores.
With a large tree, there is a tendency to overfit, therefore putting more mass at the edges.

It may be possible to find an in-between situation: solution in which the number of leaves is such that the distribution of the predicted scores is the closest to the distribution of the true probabilities.

We need to measure the distance between these two distributions: Kullback Leibler Divergence (Kullback and Leibler, 1951).

Kullback Leibler Divergence

What about accounting for the distance between the distribution of true probabilities and that of estimated scores?

To do so, we rely on the Kullback Leibler Divergence.

Kullback Leibler Divergence. (Kullback and Leibler, 1951)

For two discrete distributions $\color{wongPurple}q$ and $\color{wongLightBlue}p$, Kullback–Leibler divergence divergence of $\color{wongPurple}q$ with respect to $\color{wongLightBlue}p$ is:

\[D_{KL}({\color{wongPurple}q}||{\color{wongLightBlue}p}) = \sum_i {\color{wongPurple}q(i)} \log \frac{{\color{wongPurple}q(i)}}{{\color{wongLightBlue}p(i)}}\enspace.\]

Simulations

We want to adjust the number of leaves in the tree.

Problem: this is not a hyperparameter.

To create trees with varying numbers of leaves, we can modify two hyperparameters:

Complexity parameter
Minimum bucket size.

Divergence, Performance and Calibration

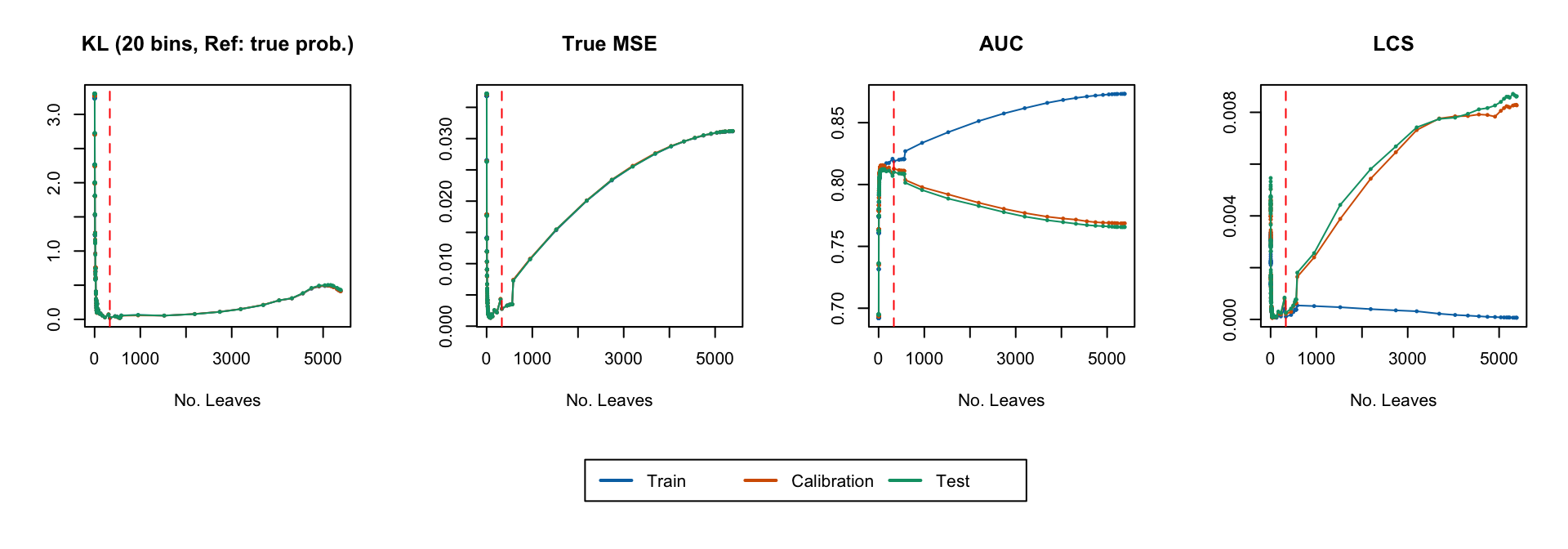
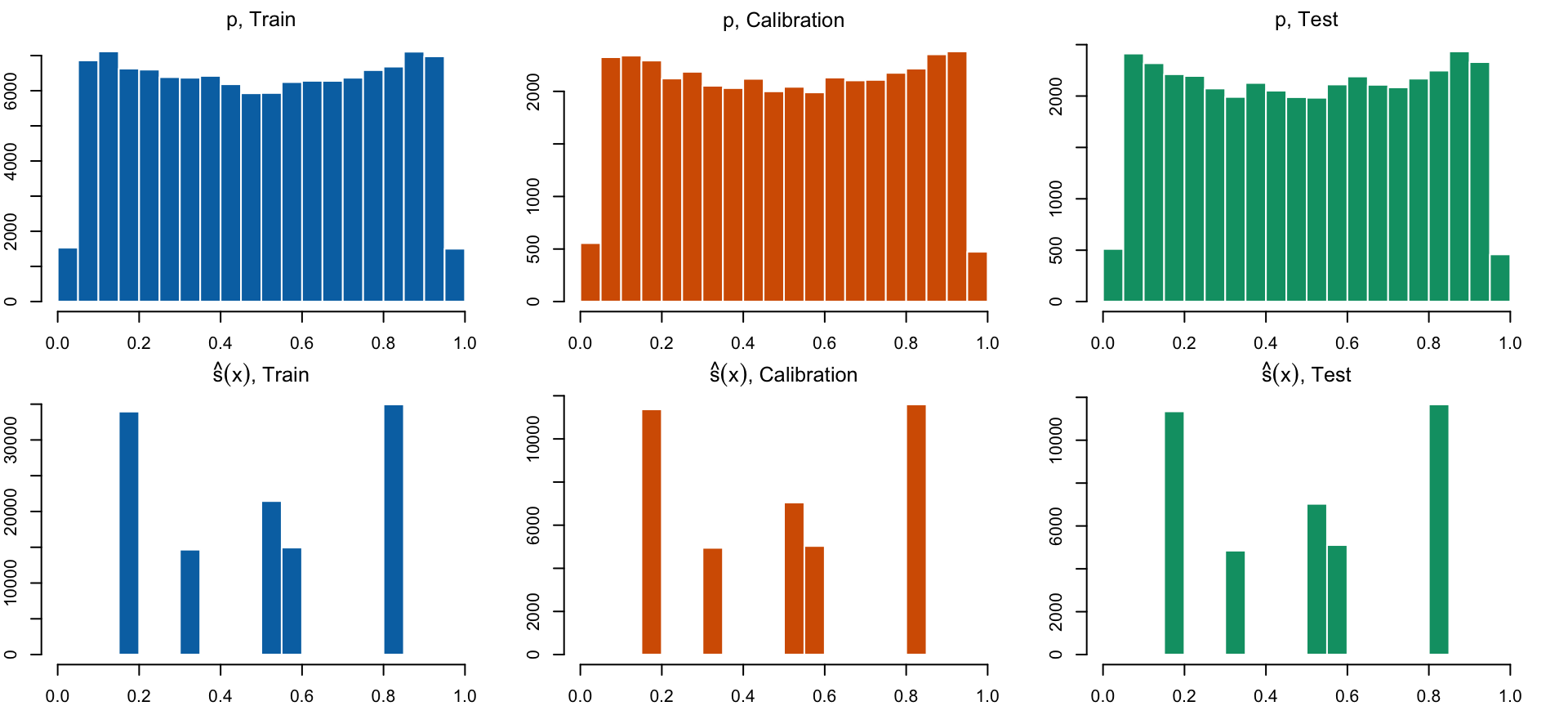
Figure 16: Divergence Metric, Performance and Calibration for Varying Number of Leaves in the Tree. Vertical red line: lowest KL with True Proba as reference.

Distribution of Predicted Scores

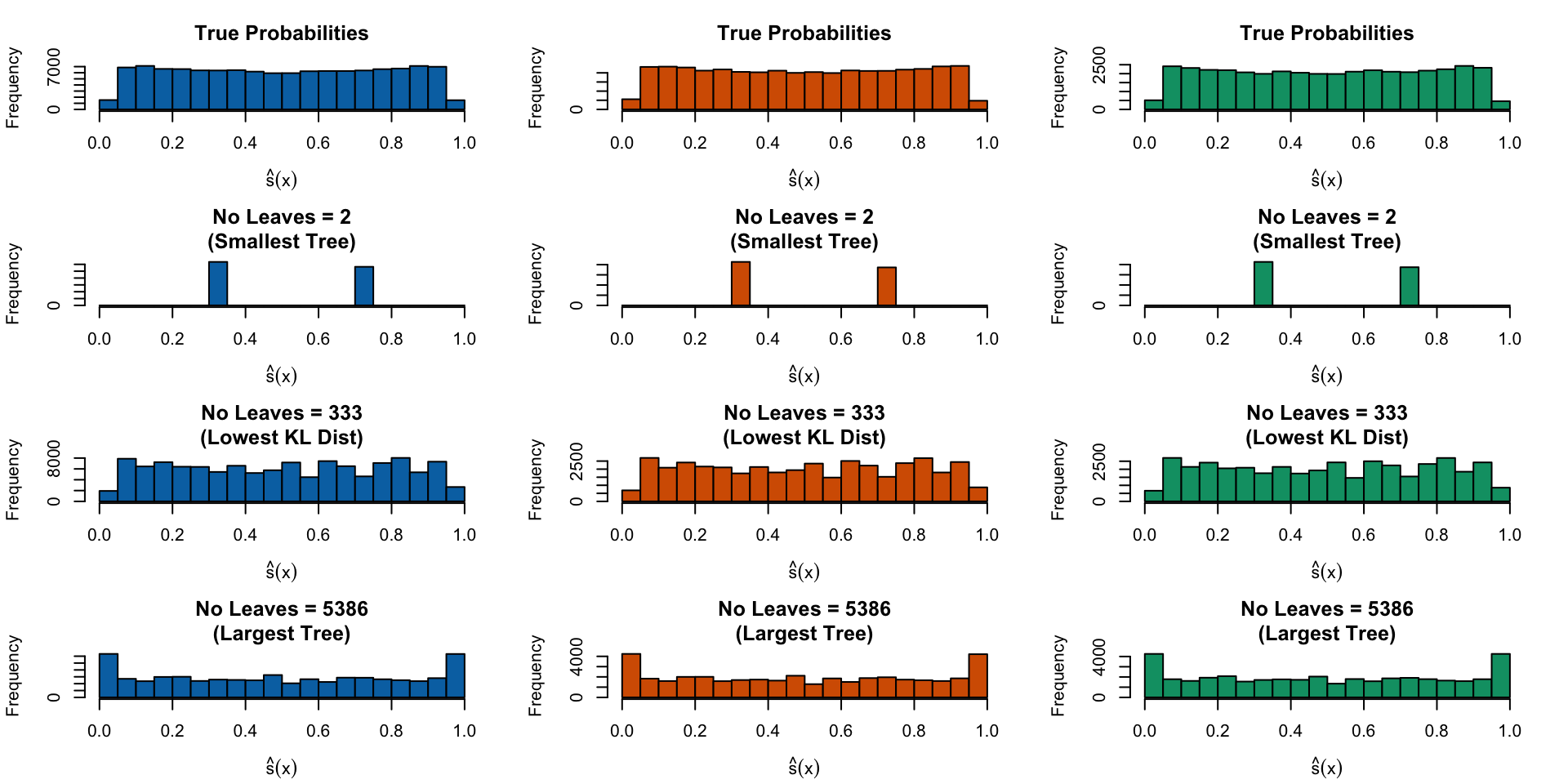
Figure 17: Distribution of true probabilities (top), estimated scores for the smallest tree (second row), for the tree with the smalled Kullback Leibler divergence (third row), and for the largest tree, when the minimal observations in terminal nodes is set to 1/1,000 of the number of observations in the train set.

6 Conclusion

Wrap up

When using predicted scores from a binary classifier, calibration matters.
Looking at usual standard performance metrics is not enough.
Even looking at calibration metrics might not be enough.
We need to further explore the relationship between tree depth, calibration and scores distributions.
We plan to continue working on tree-based methods, to explore ensemble methods such as random forests and boosting methods.

References

Bai, Y., Mei, S., Wang, H., and Xiong, C. (2021). Don’t just blame over-parametrization for over-confidence: Theoretical analysis of calibration in binary classification. International Conference on Machine Learning : 566–576.

Breiman, L. (1984). Classification and regression trees. Wadsworth International Group.

Brier, G. W. (1950). Verification of forecasts expressed in terms of probability. Monthly Weather Review 78: 1–3.

Calster, B. V., David J. McLernon, and, Smeden, M. van, Wynants, L., and Steyerberg, E. W. (2019). Calibration: The achilles heel of predictive analytics. BMC Medicine 17.

Dawid, A. P. (1982). The well-calibrated bayesian. Journal of the American Statistical Association 77: 605–610.

Gutman, R., Karavani, E., and Shimoni, Y. (2022). Propensity score models are better when post-calibrated. https://arxiv.org/abs/2211.01221, last accessed

Hill, K., and White, J. (2020). Designed to deceive: Do these people look real to you? The New York Times 11.

Krüger, F., and Ziegel, J. F. (2020). Generic conditions for forecast dominance. Journal of Business & Economic Statistics 39: 972–983.

Kull, M., Filho, T. M. S., and Flach, P. (2017). Beyond sigmoids: How to obtain well-calibrated probabilities from binary classifiers with beta calibration. Electronic Journal of Statistics 11: 5052–5080.

Kull, M., Silva Filho, T. M., and Flach, P. (2017). Beyond sigmoids: How to obtain well-calibrated probabilities from binary classifiers with beta calibration. Electronic Journal of Statistics 11.

Kullback, S., and Leibler, R. A. (1951). On information and sufficiency. The Annals of Mathematical Statistics 22: 79–86.

Loader, C. (1999). Fitting with LOCFIT. In Local regression and likelihood. New York, NY: Springer New York, 45–58.

Machado, A. F., Hu, F., Ratz, P., Gallic, E., and Charpentier, A. (2024). Geospatial disparities: A case study on real estate prices in paris. https://arxiv.org/abs/2401.16197, last accessed

Pakdaman Naeini, M., Cooper, G., and Hauskrecht, M. (2015). Obtaining well calibrated probabilities using bayesian binning. Proceedings of the AAAI Conference on Artificial Intelligence 29: 2901–2907.

Platt, J. et al. (1999). Probabilistic outputs for support vector machines and comparisons to regularized likelihood methods. Advances in Large Margin Classifiers 10: 61–74.

Schervish, M. J. (1989). A General Method for Comparing Probability Assessors. The Annals of Statistics 17: 1856–1879.

Wenger, J., Kjellström, H., and Triebel, R. (2020). Non-parametric calibration for classification. Proceedings of the 23rd International Conference on Artificial Intelligence and Statistics (AISTATS). https://github.com/JonathanWenger/pycalib, last accessed

Wilks, D. S. (1990). On the combination of forecast probabilities for consecutive precipitation periods. Weather and Forecasting 5: 640–650.

Zadrozny, B., and Elkan, C. (2002, July). Transforming classifier scores into accurate multiclass probability estimates. Proceedings of the Eighth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. http://dx.doi.org/10.1145/775047.775151, last accessed