Brefs rappels

• Étude de la liaison entre une variable \(y\) et une ou plusieurs autres \(x_1, x_2, \ldots, x_m\) ;
• \(y\) : variable à expliquer ;
• \(x_j\), \(j = 1, 2, \ldots, m\) : variables explicatives ;
• Supposition d'une relation de type : \(y = f(x_1, x_2, \ldots, x_m)\) ;
• \(m\) : nombre de variables explicatives ;
• Hypothèse : la réponse est linéairement indépendante des variables explicatives ;
• Objectif : estimer les coefficients \(\beta_j\) de l'équation à \(m\) variables explicatives \(x_j\), avec \(j = 1, \ldots, m\) :

\[\boldsymbol y = \beta_0 + \beta_1 \boldsymbol x_1 + \beta_2 \boldsymbol x_2 + \cdots + \beta_j \boldsymbol x_j + \cdots + \beta_m \boldsymbol x_m + \boldsymbol \varepsilon,\]

• \(\beta_0\) : constante ;
• \(\varepsilon\) un terme d'erreur supposé normal.

• Soit, en termes matriciels : \[\boldsymbol y = \boldsymbol X \boldsymbol \beta + \boldsymbol \varepsilon,\] \[ \textrm{où } \boldsymbol y = \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{bmatrix}, \, \boldsymbol X = \begin{bmatrix} 1 & x_{11} & x_{12} & \cdots & x_{1m} \\ 1 & x_{21} & x_{22} & \cdots & x_{2m} \\ 1 & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{n1} & x_{n2} & \cdots & x_{nm} \end{bmatrix}, \, \boldsymbol \beta = \begin{bmatrix} \beta_0\\ \beta_1\\ \beta_2\\ \vdots\\ \beta_m \end{bmatrix} \textrm{ et } \boldsymbol \varepsilon = \begin{bmatrix} \varepsilon_1\\ \varepsilon_2\\ \vdots\\ \varepsilon_m \end{bmatrix}. \]

• Les coefficients \(\beta_j\) sont inconnus et estimés par \(\hat{\beta}_j\) tels que : \[ \begin{cases} \hat{y_1} & = \hat{\beta}_{0} +\hat{\beta}_1 x_{11} + \hat{\beta}_2 x_{12} + \cdots + \hat{\beta}_j x_{1j} + \hat{\beta}_m x_{1m}\\ \hat{y_2} & = \hat{\beta}_{0} + \hat{\beta}_1 x_{21} + \hat{\beta}_2 x_{22} + \cdots + \hat{\beta}_j x_{2j} + \hat{\beta}_m x_{2m}\\ \vdots & = \vdots\\ \hat{y_n} & = \hat{\beta}_{0} + \hat{\beta}_1 x_{n1} + \hat{\beta}_2 x_{n2} + \cdots + \hat{\beta}_j x_{nj} + \hat{\beta}_m x_{nm}\\ \end{cases}. \]

• Soit, en termes matriciels : \[\hat{\boldsymbol y} = \boldsymbol X \hat{\boldsymbol \beta},\]

\[ \textrm{où } \hat{\boldsymbol y} = \begin{bmatrix} \hat{y}_1 \\ \hat{y}_2 \\ \vdots \\ \hat{y}_n \end{bmatrix}, \, \boldsymbol X = \begin{bmatrix} 1 & x_{11} & x_{12} & \cdots & x_{1m} \\ 1 & x_{21} & x_{22} & \cdots & x_{2m} \\ 1 & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{n1} & x_{n2} & \cdots & x_{nm} \end{bmatrix}, \textrm{ et } \hat{\boldsymbol \beta} = \begin{bmatrix} \hat{\beta}_0\\ \hat{\beta}_1\\ \hat{\beta}_2\\ \vdots\\ \hat{\beta}_m \end{bmatrix}. \]

• Avec les MCO, on cherche \(\hat{\boldsymbol\beta}\) tels que la somme des carr\'es des r\'esidus soit minimale ;

• La somme des carrés des résidus est définie par : \[\mid \mid \boldsymbol y - \boldsymbol X \boldsymbol \beta \mid \mid^2 = \sum_{i=1}^{n} (y_i - x_i \beta)^2.\]

• La condition du premier ordre donne : \[ \boldsymbol X^t \boldsymbol X\hat{\boldsymbol \beta} - 2 \boldsymbol X^t \boldsymbol X \hat{\boldsymbol \beta} - 2 \boldsymbol X^t \boldsymbol y = 0\notag\\ \Leftrightarrow \quad \boldsymbol X^t \boldsymbol X \hat{\boldsymbol\beta} = \boldsymbol X^t \boldsymbol y\notag\\ \Leftrightarrow \quad \hat{\boldsymbol\beta} = (\boldsymbol X^t \boldsymbol X)^{-1} \boldsymbol X^t \boldsymbol y. \]

Données de l'exemple

• Données de naissances à Philadelphie, en 1990 ;
• Elo, I., Rodgriguez, G., & Lee, H. (2001). Racial and neighborhood disparities in birth weight in philadelphia. In Annual meeting of the populations association of america, washington dc. paper presented, under revision for publication ;
• \(5\%\) des naissances ayant eu lieu dans cette ville en 1990 : \(1115\) observations ;
• Données sur :
  • grams : masse à la naissance (grammes),
  • gestate : temps de gestation (semaines),
  • educ : nombre d’années d’éducation de la mère (0–17),
  • black : variable indicatrice de la couleur de peau de la mère (1 si oui, 0 sinon),
  • smoke : indique si la mère a fumé pendant la grossesse (1 si oui, 0 sinon).

url <- "http://data.princeton.edu/wws509/datasets/phbirths.dat"
births <- read.table(url, header = TRUE)

head(births)

##   black educ smoke gestate grams
## 1 FALSE    0  TRUE      40  2898
## 2  TRUE    0  TRUE      26   994
## 3 FALSE    2 FALSE      38  3977
## 4 FALSE    2  TRUE      37  3040
## 5 FALSE    2 FALSE      38  3523
## 6 FALSE    5  TRUE      40  3100

summary(births)

##    black              educ         smoke            gestate          grams     
##  Mode :logical   Min.   : 0.00   Mode :logical   Min.   :20.00   Min.   : 284  
##  FALSE:453       1st Qu.:11.00   FALSE:846       1st Qu.:38.00   1st Qu.:2900  
##  TRUE :662       Median :12.00   TRUE :269       Median :39.00   Median :3267  
##  NA's :0         Mean   :12.27   NA's :0         Mean   :38.84   Mean   :3220  
##                  3rd Qu.:13.00                   3rd Qu.:40.00   3rd Qu.:3630  
##                  Max.   :17.00                   Max.   :43.00   Max.   :4830

• Les corrélations :

round(cor(births), 2)

##         black  educ smoke gestate grams
## black    1.00 -0.15  0.05   -0.17 -0.26
## educ    -0.15  1.00 -0.23    0.06  0.12
## smoke    0.05 -0.23  1.00   -0.15 -0.23
## gestate -0.17  0.06 -0.15    1.00  0.70
## grams   -0.26  0.12 -0.23    0.70  1.00

• Quelques graphiques

library(ggplot2)
ggplot() + geom_bar(data = births, aes(x = grams), fill = "dodger blue")

## stat_bin: binwidth defaulted to range/30. Use 'binwidth = x' to adjust this.

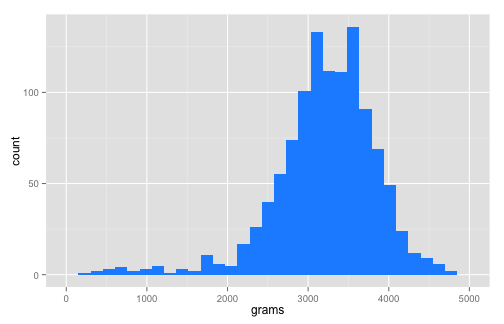
ggplot() + geom_bar(data = births, aes(x = gestate), fill = "dodger blue")

## stat_bin: binwidth defaulted to range/30. Use 'binwidth = x' to adjust this.

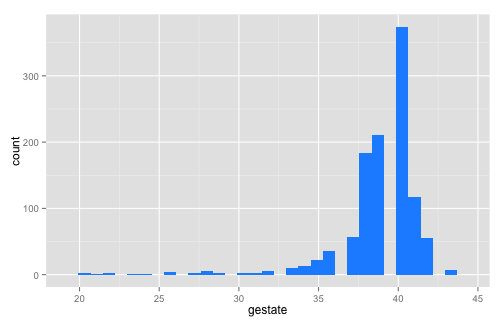
ggplot() + geom_bar(data = births, aes(x = educ), fill = "dodger blue")

## stat_bin: binwidth defaulted to range/30. Use 'binwidth = x' to adjust this.

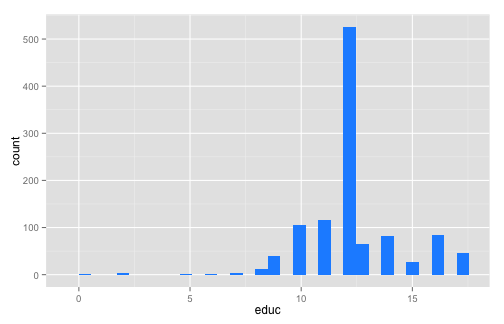
ggplot() + geom_bar(data = births, aes(x = black), fill = "dodger blue")

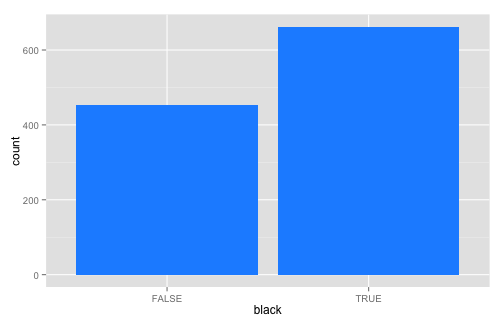
ggplot() + geom_bar(data = births, aes(x = smoke), fill = "dodger blue")

• Visualisation de toutes les observations, par variable, sous forme de nuage de points :

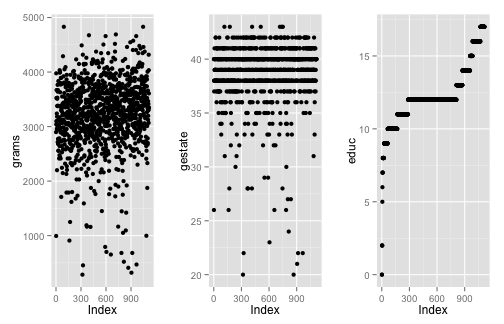
p_1 <- ggplot() + geom_point(data = births, aes(x = seq_along(grams), y = grams)) +
  xlab("Index")
p_2 <- ggplot() + geom_point(data = births, aes(x = seq_along(gestate), y = gestate)) +
  xlab("Index")
p_3 <- ggplot() + geom_point(data = births, aes(x = seq_along(educ), y = educ)) +
  xlab("Index")

library(gridExtra)
grid.arrange(p_1, p_2, p_3, ncol=3)

• Relation entre la réponse et les variables explicatives

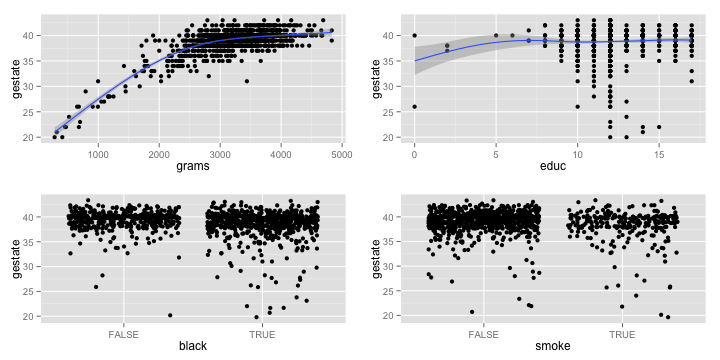
p_1 <- ggplot(data = births, aes(x = grams, y = gestate)) +
  geom_point() + geom_smooth()
p_2 <- ggplot(data = births, aes(x = educ, y = gestate)) +
  geom_point() + geom_smooth()
p_3 <- ggplot(data = births, aes(x = black, y = gestate)) +
  geom_jitter()
p_4 <- ggplot(data = births, aes(x = smoke, y = gestate)) +
  geom_jitter()

grid.arrange(p_1, p_2, p_3, p_4, ncol=2)

Estimation des paramètres

• Modèle linéaire avec R : lm() ;
• Fournir une formule ;
• Indiquer (si nécessaire) le data.frame au paramètre data.

reg <- lm(grams ~ gestate, data = births)
reg

## 
## Call:
## lm(formula = grams ~ gestate, data = births)
## 
## Coefficients:
## (Intercept)      gestate  
##     -3245.4        166.4

• Introduction d'un terme au carré : avec la fonction I() :

reg_2 <- lm(grams ~ gestate + I(gestate^2), data = births)
reg_2

## 
## Call:
## lm(formula = grams ~ gestate + I(gestate^2), data = births)
## 
## Coefficients:
##  (Intercept)       gestate  I(gestate^2)  
##    -4545.933       243.159        -1.108

Lecture des sorties

• Appliquer la fonction summary() à cet objet donne de nombreuses informations :
  • Call : la fomule du moèle,
  • Residuals : des statistiques descriptives des résidus,
  • Coefficients : un tableau à deux entrées où les lignes correspondent aux coeffcients associés aux variables explicatives, et les colonnes, dans l’ordre, à l’estimation du coefficient, l’écart-type estimé, la valeur du test de Student de nullité statistique du coeffcient et enfin la p-value associé à ce test, suivie d’un symbole pour lire rapidement la signifi- cativité,
  • Signif. codes : les significations des symboles de niveau de significativité,
  • Residual standard error : estimation de l’écart-type de l’aléa et degré de liberté,
  • Multiple R-squared : coeffcient de détermination,
  • Adjusted R-squared :coeffcient de détermination ajusté,
  • F-statistic : valeur de la statistique de Fisher du test de significativité globale, ainsi que les degrés de liberté et la p-value associée au test.

summary(reg)

## 
## Call:
## lm(formula = grams ~ gestate, data = births)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -1512.41  -302.17   -12.41   285.15  1584.04 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -3245.45     197.01  -16.47   <2e-16 ***
## gestate       166.45       5.06   32.89   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 451.3 on 1113 degrees of freedom
## Multiple R-squared:  0.4929, Adjusted R-squared:  0.4925 
## F-statistic:  1082 on 1 and 1113 DF,  p-value: < 2.2e-16

X <- matrix(c(rep(1, nrow(births)), births$gestate), ncol = 2)
y <- births$grams
(hatBeta <- solve(crossprod(X)) %*% crossprod(X,y))
yChap <- X %*% hatBeta
residus <- y - yChap
SCE <- sum((yChap - mean(y))^2)
SCT <- sum((y - mean(y))^2)
R2 <- SCE / SCT
m <- 4
n <- nrow(births)
R2a <- 1 - ((n-1) / (n-m-1)) * (1-R2)
SCR <- sum(residus^2)
hatSigma2_u <- SCR / (n-m-1)
varcov <- hatSigma2_u * solve(t(X) %*% X)
hatSigmaBetas <- sqrt(diag(varcov))
tObs <- hatBeta / hatSigmaBetas
T_tab <- qt(p = 1-0.05/2, df = n-m-1)
ifelse(abs(tObs) > T_tab, "Rejet H_0", "Non rejet H_0")
2*pt(q = abs(tObs), df = n-m-1, lower.tail=FALSE)
F_obs <- (R2 / m) / ((1-R2) / (n-m-1))
F_tab <- qf(p = 1-0.05, df1 = m, df2 = n-m-1)
1 - pf(q = F_obs, df1 = m, df2 = n-m-1)

• On peut aisément retrouver à la main tous ces résultats ;
• Voir le billet http://editerna.free.fr/wp/?p=233.

Extractions

• Lire et interpéter les sorties est une chose ;
• Pouvoir les réutiliser en est une autre ;
• Il est important de savoir comment accéder aux éléments issus de la régression, dont les principaux sont :
  • coefficients : un vecteur de coeffcients (nommé),
  • resiuals : les résidus,
  • fitted.values : les valeurs estimées,
  • df.residual : nombre de degrés de liberté.

• La liste totale est accessibles via la fonction names() :

names(reg)

##  [1] "coefficients"  "residuals"     "effects"       "rank"         
##  [5] "fitted.values" "assign"        "qr"            "df.residual"  
##  [9] "xlevels"       "call"          "terms"         "model"

• Il suffit alors d'extraire l'élément souhaité, en l'appelant par son nom :

reg$coefficients

## (Intercept)     gestate 
##  -3245.4464    166.4463

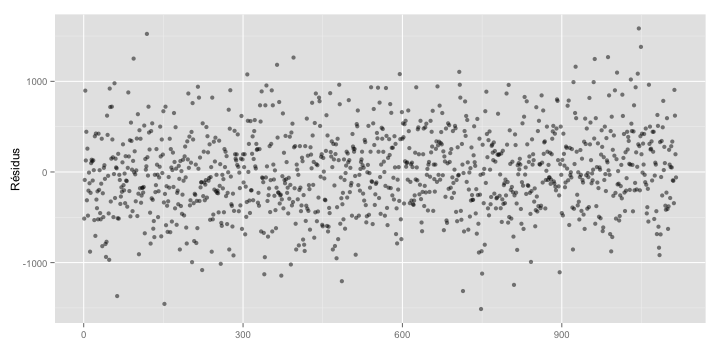
ggplot() + geom_point(data = data.frame(residuals = reg$residuals), 
                      aes(x = seq_along(residuals), y = residuals), alpha = .5) +
  xlab("") + ylab("Résidus")

• En ordonnant en fonction de la masse des nouveaux nés :

library(plyr)
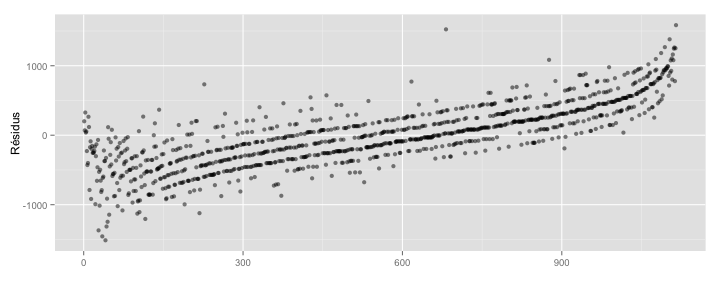
ggplot() + geom_point(data = arrange(data.frame(residuals = reg$residuals,
                                                grams = births$grams), grams), 
                      aes(x = seq_along(residuals), y = residuals), alpha = .5) +
  xlab("") + ylab("Résidus")

• Accès aux résidus :
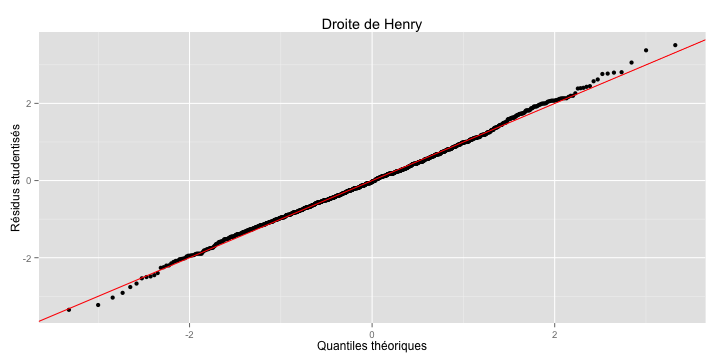
  • residuals(reg),
  • resid(reg),
  • reg$residuals ;
• Accès aux valeurs estimées :
  • fitted(reg) ;
• Accès aux coefficients :
  • coefficients(reg),
  • coef(reg),
  • reg$coefficients

• Mise en pratique : tracer la droite de Henry :

qqplot <- function(y, distribution=qnorm, title = "Droite de Henry",
                   xlab = "Quantiles théoriques",
                   ylab = "Résidus studentisés") {
  if(class(y) == "lm"){
    # Résidus
    r <- residuals(y)
    # Résidus studentisés
    y <- r / sqrt(deviance(y) / df.residual(y))
  }
  x <- distribution(ppoints(y))
  df <- data.frame(x = x, y = sort(y))
  ggplot(df, aes(x = x, y = y)) +
    geom_point() +
    geom_abline(intercept = 0, slope = 1, col = "red") +
    ggtitle(title) +
    xlab(xlab) + ylab(ylab)
}

qqplot(reg)

Variables catégorielles

Source : stux

• Les variables catégorielles sont de mode factor ;
• Deux méthodes pour les intégrer à un modèle de régression dans R :
  • définir a priori la variable en facteur dans le data.frame,
  • appliquer la fonction factor() dans la formule, lors de l'appel de la régression ;
• Si la variable est de type character ou logical, R la transforme en factor durant le temps de l'estimation ;
• Attention, la modalité de référence est définie en fonction de l'ordre alphanumérique en R ;
• Cette modalité de référence peut-être bien évidemment changée, à l'aide de la fonction relevel(), ou directement avec factor().

class(births$smoke)

## [1] "logical"

summary(reg_3 <- lm(grams ~ gestate + smoke + black, data = births))

## 
## Call:
## lm(formula = grams ~ gestate + smoke + black, data = births)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -1464.13  -295.56     1.86   287.70  1611.83 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -2713.653    199.723 -13.587  < 2e-16 ***
## gestate       156.570      5.016  31.213  < 2e-16 ***
## smokeTRUE    -185.015     30.883  -5.991 2.82e-09 ***
## blackTRUE    -174.402     27.027  -6.453 1.64e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 436.3 on 1111 degrees of freedom
## Multiple R-squared:  0.5269, Adjusted R-squared:  0.5256 
## F-statistic: 412.4 on 3 and 1111 DF,  p-value: < 2.2e-16

• En laissant R faire en fonction de l'ordre alphanumérique :

births$smoke <- factor(births$smoke)
levels(births$smoke)

## [1] "FALSE" "TRUE"

• En imposant la modalité TRUE comme référence :

births$smoke <- relevel(births$smoke, ref = "TRUE")

• En utilisant la fonction factor() pour définir la référence et d'éventuelles étiquettes :

births$black <- factor(births$black, levels = c("TRUE", "FALSE"),
                       labels = c("Black", "Not Black"))

summary(reg_3 <- lm(grams ~ gestate + smoke + black, data = births))

## 
## Call:
## lm(formula = grams ~ gestate + smoke + black, data = births)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -1464.13  -295.56     1.86   287.70  1611.83 
## 
## Coefficients:
##                 Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    -3073.071    191.836 -16.019  < 2e-16 ***
## gestate          156.570      5.016  31.213  < 2e-16 ***
## smokeFALSE       185.015     30.883   5.991 2.82e-09 ***
## blackNot Black   174.402     27.027   6.453 1.64e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 436.3 on 1111 degrees of freedom
## Multiple R-squared:  0.5269, Adjusted R-squared:  0.5256 
## F-statistic: 412.4 on 3 and 1111 DF,  p-value: < 2.2e-16

Tests de nullité des coefficients

Source : PhD Comics : http://www.phdcomics.com/comics.php?f=1457

• Le problème de test est le suivant :

\[ \begin{cases} H_0 : \beta_i = 0\\ H_1 : \beta_i \ne 0 \end{cases}, i = 1, 2, \ldots, m. \]

• La statistique de test est la suivante : \[ T = \frac{\hat{\beta}_i - \beta_{i,H_0}}{\hat{\sigma}_{\hat{\beta}_i}} \sim \mathcal{S}t(n-m-1,)\]
• avec \(\beta_{i,H_0}\) la valeur de \(\beta_j\) sous l'hypothèse nulle ;
• \(\hat{\sigma}_{\hat{\beta}_i}\) l'estimation de l'écart-type de l'estimation du paramètre \(\beta_i\).

• Pour effectuer ce test bilatéeral, on peut lire dans la table de la loi de Student deux fractiles tels que : \[ \mathbb{P}\left( -t_{1-\alpha/2} < \frac{\hat{\beta}_i - \alpha_{i,H_0}}{\hat{\sigma}_{\hat{\beta}_i}} < t_{1-\alpha/2} \right) = 1 - \alpha. \]
• avec \(\alpha\) le risque de première espèce ;
• À partir des observations, il est possible de calculer : \[ t_{i,\textrm{obs.}} = \frac{\hat{\beta}_i}{\hat{\sigma}_{\hat{\beta}_i}}. \]

• Les tests de nullité des coefficients sont effectués lors de l'appel de summary() sur l'objet retourné par la fonction lm() ;
• Pour décider du rejet ou non de l'hypothèse de nullité d'un coefficient, on peut :
  • se baser sur la valeur de la statistique en la comparant à la valeur tabulée,
  • se baser sur la p-value,
  • regarder si 0 appartient à l'intervalle de confiance ;
• Pour obtenir les intervalles de confiance des coefficients de la régression, on peut utiliser la fonction confint() :

• Avec un niveau à \(95\%\) par défaut :

confint(reg_3)

##                     2.5 %     97.5 %
## (Intercept)    -3449.4726 -2696.6686
## gestate          146.7278   166.4120
## smokeFALSE       124.4204   245.6101
## blackNot Black   121.3724   227.4324

• En précisant le niveau :

confint(reg_3, level = 0.95)

##                     2.5 %     97.5 %
## (Intercept)    -3449.4726 -2696.6686
## gestate          146.7278   166.4120
## smokeFALSE       124.4204   245.6101
## blackNot Black   121.3724   227.4324

Prévisions

Source : Minority Report

• Il arrive de vouloir appliquer le modèle estimé à de nouvelles observations, afin d'effectuer des prévisions ;
• On considère un nouvel enregistrement, \(\boldsymbol{x}^\top_{n+1} = \begin{bmatrix} x_{n+1, 1} & x_{n+1, 2} & \ldots & x_{n+1, m} \end{bmatrix}\) ;
• L'objectif est de prévoir la valeur de \(y_{n+1}\), en utilisant la relation initiale : \[ y_{n+1} = \beta_0 + \beta_1 \boldsymbol x_{n+1,1} + \beta_2 \boldsymbol x_{n+1,2} + \cdots + \beta_m \boldsymbol x_{n+1,m} + \boldsymbol \varepsilon_{n+1}.\label{eq:regressions_previsions}, \]
• où \(\mathbb{E}[\varepsilon_{n+1}] = 0\) ;
• \(\mathbb{V}(\varepsilon_{n+1}) = \sigma^2\) ;
• \(\mathbb{C}ov(\varepsilon_{n+1}, \varepsilon_{i}) = 0\), \(i = 1, 2, \ldots, n\).

• La valeur prévue, \(\hat y_{n+1}^p\) s'appuie sur les coefficients estim\'es par le modèle :
• \[ \hat y_{n+1}^p = \hat\beta_0 + \hat\beta_1 \boldsymbol x_{n+1,1} + \hat\beta_2 \boldsymbol x_{n+1,2} + \cdots + \hat\beta_m \boldsymbol x_{n+1,m}. \]
• On note \(z_{n+1} = y_{n+1} - \hat y_{n+1}^p\) l'erreur de prévision. On a : \[ \begin{cases} \mathbb{E}[z_{n+1}] = 0\\ \mathbb{V}(z_{n+1}) = \sigma^2 \times \left( 1 + \boldsymbol {x}^\top_{n+1} (\boldsymbol X^\top \boldsymbol X)^{-1} \boldsymbol x_{n+1} \right) \end{cases} \]
• Comme on émet l'hypothèse que la distribution des \(\varepsilon_i\) est normale, la distribution des \(y_{i}\) et \(\hat y_{i}^p\) l'est aussi ;
• De fait, on a : \[ z_i^p \sim \mathcal{N}\left(0,\sqrt{\mathbb{V}(z_i^p)}\right). \]

• On peut estimer la variance inconnue \(\sigma^2_\varepsilon\) par son estimation \(\hat{\sigma}^2_\varepsilon\).

• Dès lors, on a : \[ \frac{z_i^p - \mathbb{E}(z_i^p)}{\hat{\sigma}_{\varepsilon}} \sim \mathcal{S}t(n-2). \]

• Il est alors possible de construire un intervalle de confiance au seuil de \(\alpha\) pour \(y_i^p\), soit : \[ \widehat{\textrm{I.C.}_{y_{n+1}}(1-\alpha)} = \left[ \hat{y}_{n+1}^p \pm t_{1-\alpha/2} \cdot \hat{\sigma}_{z_{n+1}^p} \right], \]

• où \(t_{1-\alpha/2}\) est la valeur du fractile lue dans la table pour \(\alpha\) et \(\gamma = n-2\) degrés de liberté.

• R propose la fonction predict() pour calculer cet intervalle de prévision ;
• Il faut passer l'objet retourné par lm() en paramètre ;
• Et préciser un data.frame contenant les nouvelles valeurs (sinon, predict() retourne les valeurs estimées) ;
• Il faut toutefois faire attention à conserver les mêmes noms de variable dans le nouveau data.frame que ceux passés dans la formule.

donnees_supl <- data.frame(black = factor(c(TRUE, FALSE),
                                          levels = c(TRUE, FALSE),
                                          labels = c("Black", "Not Black")),
                           educ = c(10,5),
                           smoke = factor(c(FALSE, FALSE)),
                           gestate = c(39, 43))
predict(reg_3, newdata = donnees_supl)

##        1        2 
## 3218.171 4018.853

• Les intervalles de confiance peuvent être donnés ;
• Il faut pour ce faire donner la valeur "prediction" au paramètre interval ;
• Par défaut, l'intervalle est donné pour un niveau de \(95\%\) ;
• Le paramètre level permet de spécifier un niveau différent.

predict(reg_3, newdata = donnees_supl, interval = "prediction")

##        fit      lwr      upr
## 1 3218.171 2361.229 4075.113
## 2 4018.853 3161.006 4876.700

• Avec l'I.C. à \(90\%\) :

predict(reg_3, newdata = donnees_supl, interval = "prediction", level = 0.9)

##        fit      lwr      upr
## 1 3218.171 2499.187 3937.155
## 2 4018.853 3299.109 4738.597

• Les écarts-types peuvent être retournés, en donnant la valeur TRUE au paramètre se.fit :

predict(reg_3, newdata = donnees_supl, interval = "prediction", se.fit = TRUE)

## $fit
##        fit      lwr      upr
## 1 3218.171 2361.229 4075.113
## 2 4018.853 3161.006 4876.700
## 
## $se.fit
##        1        2 
## 18.79725 27.50835 
## 
## $df
## [1] 1111
## 
## $residual.scale
## [1] 436.3423

Exportation des résultats

Source : PhD Comics : http://www.phdcomics.com/comics/archive.php?comicid=814

• Les sorties dans la console sont pratiques pour réaliser l'analyse ;
• Il est peu esthétique de copier/coller ces résultats dans un document, tels quels ;
• Le package texreg propose des fonctions pour exporter les résultat de régression :
  • en HTML : htmlreg(),
  • en LaTeX : texreg ;
• À partir d'un document HTML, il est aisé de copier/coller un tableau dans Word...

• Les paramètres principaux de ces fonctions sont :
  • l : un modèle statistique, ou une liste de modèles,
  • file : le résultat est exporté dans un fichier dont le chemin et le nom sont donnés à ce paramètre,
  • single.row : par défaut, deux lignes sont réservées par coeffcient de la régression, avec le coeffcient sur la première ligne, et l’écart-type sur la seconde. Si la valeur vaut TRUE, le coeffcient et son écart-type sont placés dans une celle cellule, sur la même ligne,
  • custom.model.names : un vecteur de caractères avec les étiquettes pour chaque modèle (au lieu de "Model 1", "Model 2", etc.),
  • custom.coef.names : un vecteur de caractères avec les étiquettes pour chaque variable du modèle,
  • digits : nombre de décimales,
  • caption : titre pour le tableau.

• En affichant dans la console :

library(texreg)
htmlreg(reg_3, digits = 2, caption = "Résultats de la régression")
texreg(reg_3, digits = 2, caption = "Résultats de la régression")

• En exportant les résultats dans un fichier :

htmlreg(reg_3, file = "reg_3.html") texreg(reg_3, file = "reg_3.tex")

• La fonction screenreg propose d'afficher dans la console un aperçu de ce à quoi ressemblera la sortie :

screenreg(list(reg, reg_3), digits = 2,
          custom.model.names = c("Rég. Lin. Simple", "Reg. Lin. Mult."))